Article contents
Cardinal invariants and the collapse of the continuum by Sacks forcing
Published online by Cambridge University Press: 12 March 2014
Abstract
We study cardinal invariants of systems of meager hereditary families of subsets of ω connected with the collapse of the continuum by Sacks forcing 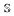 and we obtain a cardinal invariant
and we obtain a cardinal invariant 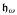 such that
such that 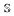 collapses the continuum to
collapses the continuum to 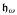 and
and 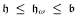 . Applying the Baumgartner-Dordal theorem on preservation of eventually narrow sequences we obtain the consistency of
. Applying the Baumgartner-Dordal theorem on preservation of eventually narrow sequences we obtain the consistency of 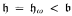 . We define two relations
. We define two relations 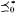 and
and 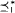 on the set (ωω)Fin of finite-to-one functions which are Tukey equivalent to the eventual dominance relation of functions such that if
on the set (ωω)Fin of finite-to-one functions which are Tukey equivalent to the eventual dominance relation of functions such that if 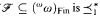 -unbounded, well-ordered by
-unbounded, well-ordered by 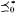 , and not
, and not 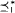 -dominating, then there is a nonmeager p-ideal. The existence of such a system
-dominating, then there is a nonmeager p-ideal. The existence of such a system 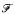 follows from Martin's axiom. This is an analogue of the results of [3], [9, 10] for increasing functions.
follows from Martin's axiom. This is an analogue of the results of [3], [9, 10] for increasing functions.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2008
References
REFERENCES
- 2
- Cited by

