No CrossRef data available.
Article contents
CHAITIN’S Ω AS A CONTINUOUS FUNCTION
Published online by Cambridge University Press: 09 September 2019
Abstract
We prove that the continuous function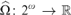 ${\rm{\hat \Omega }}:2^\omega \to $ that is defined via
${\rm{\hat \Omega }}:2^\omega \to $ that is defined via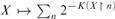 $X \mapsto \mathop \sum \limits_n 2^{ - K\left( {Xn} \right)} $ for all
$X \mapsto \mathop \sum \limits_n 2^{ - K\left( {Xn} \right)} $ for all 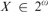 $X \in {2^\omega }$ is differentiable exactly at the Martin-Löf random reals with the derivative having value 0; that it is nowhere monotonic; and that
$X \in {2^\omega }$ is differentiable exactly at the Martin-Löf random reals with the derivative having value 0; that it is nowhere monotonic; and that 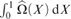 $\mathop \smallint \nolimits _0^1{\rm{\hat{\Omega }}}\left( X \right)\,{\rm{d}}X$ is a left-c.e.
$\mathop \smallint \nolimits _0^1{\rm{\hat{\Omega }}}\left( X \right)\,{\rm{d}}X$ is a left-c.e. 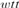 $wtt$-complete real having effective Hausdorff dimension
$wtt$-complete real having effective Hausdorff dimension 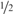 ${1 / 2}$.
${1 / 2}$.
We further investigate the algorithmic properties of 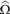 ${\rm{\hat{\Omega }}}$. For example, we show that the maximal value of
${\rm{\hat{\Omega }}}$. For example, we show that the maximal value of 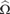 ${\rm{\hat{\Omega }}}$ must be random, the minimal value must be Turing complete, and that
${\rm{\hat{\Omega }}}$ must be random, the minimal value must be Turing complete, and that 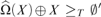 ${\rm{\hat{\Omega }}}\left( X \right) \oplus X{ \ge _T}\emptyset \prime$ for every X. We also obtain some machine-dependent results, including that for every
${\rm{\hat{\Omega }}}\left( X \right) \oplus X{ \ge _T}\emptyset \prime$ for every X. We also obtain some machine-dependent results, including that for every 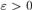 $\varepsilon > 0$, there is a universal machine V such that
$\varepsilon > 0$, there is a universal machine V such that 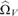 ${{\rm{\hat{\Omega }}}_V}$ maps every real X having effective Hausdorff dimension greater than ε to a real of effective Hausdorff dimension 0 with the property that
${{\rm{\hat{\Omega }}}_V}$ maps every real X having effective Hausdorff dimension greater than ε to a real of effective Hausdorff dimension 0 with the property that 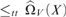 $X{ \le _{tt}}{{\rm{\hat{\Omega }}}_V}\left( X \right)$; and that there is a real X and a universal machine V such that
$X{ \le _{tt}}{{\rm{\hat{\Omega }}}_V}\left( X \right)$; and that there is a real X and a universal machine V such that  ${{\rm{\Omega }}_V}\left( X \right)$ is rational.
${{\rm{\Omega }}_V}\left( X \right)$ is rational.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019

