Article contents
Changing cofinalities and infinite exponents1,2
Published online by Cambridge University Press: 12 March 2014
Extract
Ever since Cohen invented forcing in 1963, people have studied the properties that cardinals can have in generic extensions of the ground model. A very early result of Lévy shows that if κ is a regular cardinal and λ > κ is strongly inaccessible, then there is a notion of forcing which collapses every cardinal strictly between κ and λ yet preserves every other cardinal. This, of course, answers one question of the genre “What properties can a cardinal have in a generic extension?”
Another question of the same genre that can be asked is the following: Is it possible to have a generic extension of the ground model in which all cardinals are preserved and yet the cofinalities of some cardinals are different? This question was first answered in the affirmative by Prikry, who proved the following theorem.
Theorem 1.1 (Prikry [5]). Assume that V ⊨ “ZFC + κ is measurable”. Then there is a notion of forcing, P, such that for G V-generic over P:
(1) V and V[G] have the same cardinals.
(2) V and V[G] have the same bounded subsets of κ.
(3) V[G]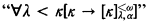 , i.e, V[G] ⊨ “κ is Rowbottom”.
, i.e, V[G] ⊨ “κ is Rowbottom”.
(4) V[G] ⊨ “cof(κ) = ω”.
Prikry's result naturally raises the following question: Is it possible to get a generic extension in which cardinals are preserved and yet the cofinalities of certain cardinals are different from the ground model's but are uncountable? This question was first answered in the affirmative by Magidor, who proved the following theorem.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1981
Footnotes
The results obtained in this paper form a portion of the author's doctoral dissertation written at M.I.T. under Professor E. M. Kleinberg, to whom the author is indebted for his aid and encouragement.
The author wishes to express his gratitude to the referee of this paper for helpful comments and useful suggestions which considerably improved presentation of the material contained herein.
References
REFERENCES
- 1
- Cited by

