Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mildenberger, Heike
and
Shelah, Saharon
2014.
Many countable support iterations of proper forcings preserve Souslin trees.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 2,
p.
573.
Pawlikowski, Janusz
and
Stadnicki, Wojciech
2020.
Playing with Mathias.
Topology and its Applications,
Vol. 285,
Issue. ,
p.
107387.

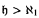 is consistent. We work with a class of axiom
is consistent. We work with a class of axiom 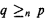 is determined by finitely many elements in the conditions
is determined by finitely many elements in the conditions 