Hostname: page-component-7dd5485656-kp629 Total loading time: 0 Render date: 2025-10-30T18:50:53.195Z Has data issue: false hasContentIssue false
  • English
  • Français

Coding over a measurable cardinal

Published online by Cambridge University Press:  12 March 2014

Sy D. Friedman
Sy D. Friedman*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of this paper is to extend the coding method (see Beller, Jensen and Welch [82]) into the context of large cardinals.

Theorem. Suppose μ is a normal measure on κ in V and 〈 V, A〉 ⊨ ZFC. Then there is a 〈V, A〉-definable forcing 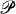for producing a real R such that:

(a) V[R] ⊨ ZFC and A is V[R]-definable with parameter R.

(b) V[R] = L[μ*, R], where μ* is a normal measure on κ in V[R] extending μ.

(c) V ⊨ GCH → 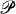is cardinal and cofinality preserving.

Corollary. It is consistent that μ is a normal measure, R ⊆ ω is not set-generic over L[μ] and 0+ ∉ L[μ, R].

Some other corollaries will be discussed in §4 of the paper.

The main difficulty in L[μ]-coding lies in the problem of “stationary restraint”.

As in all coding constructions, conditions will be of the form 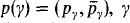belonging to an initial segment of the cardinals, where p(γ) is a condition for almost disjoint coding 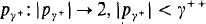into a subset of γ +. In addition for limit cardinals γ in Domain(p), 〈p γ′∣γ′ < γ〉 serves to code pγ .

An important restriction in coding arguments is that for inaccessible 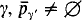for only a nonstationary set of γ′ < γ. The reason is that otherwise there are conflicts between the restraint imposed by the different 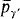and the need to code extensions of pγ below γ.

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 4 , December 1989 , pp. 1145 - 1159
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Beller, A., Jensen, R. B. and Welch, P. H. [82], Coding the universe, Cambridge University Press, Cambridge.CrossRefGoogle Scholar
David, R. [82], Some applications of Jensen's coding theorem, Annals of Mathematical Logic, vol. 22, pp. 177–196.CrossRefGoogle Scholar
David, R. [83], reals, Annals of Pure and Applied Logic, vol. 23 (1982 1), pp. 121–125.Google Scholar
Dodd, A. J. [82], The core model, Cambridge University Press, Cambridge.Google Scholar
Donder, H. D. [86], Another look at gap-1 morasses, Recursion theory, Proceedings of Symposia in Pure Mathematics, vol. 42, American Mathematical Society, Providence, Rhode Island, pp. 223–236.CrossRefGoogle Scholar
Friedman, S. D. [87], Strong coding Annals of Pure and Applied Logic, vol. 35, pp. 1–98, 99–122.CrossRefGoogle Scholar
Friedman, S. D. [89], The coding method in set theory (to appear).Google Scholar
Jech, T., Magidor, M., Mitchell, W. and Prikry, K., Precipitous ideals, this Journal, vol. 45, pp. 1–8.Google Scholar
Jensen, R. B. [68], Measurable cardinals and the GCH, Axiomatic set theory, Proceedings of Symposia in Pure Mathematics, vol. 13, part 2, American Mathematical Society, Providence, Rhode Island, 1974, pp. 175–178.CrossRefGoogle Scholar