Coinductive ℵ₀-categorical theories

Extract

Let L be a countable language which contains only constant and relation symbols but no function symbols. All theories considered here will be L-theories. A theory is coinductive if it can be axiomatized by a set of ∃∀ sentences, and a structure is coinductive if its theory is.

The object of this paper is to show that coinductive ℵ₀-categorical structures are especially simple. First, they are ω-stable with Morley rank ≤ 1; and second, they have simple algebraic closures, by which is meant that the algebraic closure of the union of two sets is the union of their algebraic closures. While these two properties do not characterize coinductive ℵ₀-categorical structures, they do characterize those structures which are cellular.

We will say that a countable structure 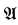is cellular if there is a finite subset A₀ ⊆ A and there are equivalence relations E and F on A∖A₀ such that the following hold:

(1) There are only finitely many E-classes.

(2) If C is an E-class and D an F-class, then ∣C ∩ D ∣ = 1.

(3) If a₀, a₁, …, a_{k − 1}, b₀, b₁, …, b_{k − 1} Є A, then 〈a₀, a₁, …,a_{k − 1}〉 and 〈b₀,b₁, …, b_{k − 1}〉, satisfy the same quantifier-free formulas provided that:

(a) if i < k and either a_i Є A₀ or b_i Є A₀, then a_i = b_i;

(b) if i < k, then a_i; and b_i are E-equivalent; and

(c) if i, j < k, then a_i; is F-equivalent to a_j if b_j is F-equivalent to b_j.

The main result of this paper is the following theorem.

Theorem 1. If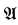is coinductive and ℵ₀-categorical, then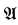is cellular.

The results of this paper were obtained independently of similar results obtained by Lachlan which can be found in [4] and [5]. The proofs here are quite different.