Article contents
Colimit completions and the effective topos
Published online by Cambridge University Press: 12 March 2014
Extract
The family of readability toposes, of which the effective topos is the best known, was discovered by Martin Hyland in the late 1970's. Since then these toposes have been used for several purposes. The effective topos itself was originally intended as a category in which various recursion-theoretic or effective constructions would live as natural parts of the higher-order type structure. For example the hereditary effective operators become the higher types over N (Hyland [1982]), and effective domains become the countably-based domains in the topos (McCarty [1984], Rosolini [1986]). However, following the discovery by Moggi and Hyland that it contained nontrivial small complete categories, the effective topos has also been used to provide natural models of polymorphic type theories, up to and including the theory of constructions (Hyland [1987], Hyland, Robinson and Rosolini [1987], Scedrov [1987], Bainbridge et al. [1987]).
Over the years there have also been several different constructions of the topos. The original approach, as in Hyland [1982], was to construct the topos by first giving a notion of Pω-valued set. A Pω-valued set is a set X together with a function =x: X × X → Pω. The elements of X are to be thought of as codes, or as expressions denoting elements of some “real underlying” set in the topos. Given a pair (x,x′) of elements of X, the set =x (x,x′) (generally written 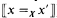 ) is the set of codes of proofs that the element denoted by x is equal to the element denoted by x′.
) is the set of codes of proofs that the element denoted by x is equal to the element denoted by x′.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1990
References
REFERENCES
- 25
- Cited by

