Hostname: page-component-7dd5485656-pnlb5 Total loading time: 0.001 Render date: 2025-10-31T12:31:30.716Z Has data issue: false hasContentIssue false
  • English
  • Français

Combinatorial principles weaker than Ramsey's Theorem for pairs

Published online by Cambridge University Press:  12 March 2014

Denis R. Hirschfeldt  and
Richard A. Shore
Denis R. Hirschfeldt
Affiliation:
Department of Mathematics, University of Chicago, Chicago, IL 60637, USA. E-mail: drh@math.uchicago.edu
Richard A. Shore
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853, USA. E-mail: shore@math.cornell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the complexity of various combinatorial theorems about linear and partial orders, from the points of view of computability theory and reverse mathematics. We focus in particular on the principles ADS (Ascending or Descending Sequence), which states that every infinite linear order has either an infinite descending sequence or an infinite ascending sequence, and CAC (Chain-AntiChain), which states that every infinite partial order has either an infinite chain or an infinite antichain. It is wellknown that Ramsey's Theorem for pairs (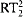) splits into a stable version (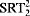) and a cohesive principle (COH). We show that the same is true of ADS and CAC, and that in their cases the stable versions are strictly weaker than the full ones (which is not known to be the case for 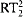and 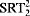). We also analyze the relationships between these principles and other systems and principles previously studied by reverse mathematics, such as WKL0, DNR, and BΣ2. We show, for instance, that WKL0 is incomparable with all of the systems we study. We also prove computability-theoretic and conservation results for them. Among these results are a strengthening of the fact, proved by Cholak, Jockusch, and Slaman, that COH is 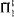-conservative over the base system RCA0. We also prove that CAC does not imply DNR which, combined with a recent result of Hirschfeldt, Jockusch. Kjos-Hanssen, Lempp, and Slaman, shows that CAC does not imply 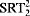(and so does not imply 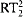). This answers a question of Cholak, Jockusch, and Slaman.

Our proofs suggest that the essential distinction between ADS and CAC on the one hand and 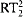on the other is that the colorings needed for our analysis are in some way transitive. We formalize this intuition as the notions of transitive and semitransitive colorings and show that the existence of homogeneous sets for such colorings is equivalent to ADS and CAC, respectively. We finish with several open questions.

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 1 , March 2007 , pp. 171 - 206
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1]Ambos-Spies, K., Kjos-Hanssen, B., Lempp, S., and Slaman, T. A., Comparing DNR and WWKL, this Journal, vol.69 (2004), pp. 1089–1104.Google Scholar
[2]Arslanov, M., Cooper, S. B., and Li, A., There is no low maximal d.c.e. degree—corrigendum, Mathematical Logic Quarterly, vol. 50 (2004), pp. 628–636.CrossRefGoogle Scholar
[3]Avigad, J., Notes on -conservativity, ω-submodels, and the collection schema, Technical Report CMU-PHIL-125, Carnegie Mellon, 2002, (updated version available at http://www.andrew.cmu.edu/user/avigad/papers.html).Google Scholar
[4]Cholak, P. A., Jockusch, C. G. Jr., and Slaman, T. A., On the strength of Ramsey's Theorem for pairs, this Journal, vol. 66 (2001), pp. 1–55.Google Scholar
[5]Cooper, S. B., Jump equivalence of the hyperhyperimune sets, this Journal, vol. 37 (1972), pp. 598–600.Google Scholar
[6]Downey, R., Hirschfeldt, D. R., Lempp, S., and Solomon, R., A set with no infinite low subset in either it or its complement, this Journal, vol.66 (2001), pp. 1371–1381.Google Scholar
[7]Downey, R. G., Computability theory and linear orderings, Handbook of recursive mathematics (Ershov, , Goncharov, , Nerode, , and Remmel, , editors), Studies in Logic and the Foundations of Mathematics, vol. 138–139, Elsevier, Amsterdam, 1998, pp. 823–976.Google Scholar
[8]Friedman, H., Systems of second order arithmetic with restricted induction I (abstract), this Journal, vol. 41 (1976), pp. 557–558.Google Scholar
[9]Giusto, M. and Simpson, S. G., Located sets and reverse mathematics, this Journal, vol. 65 (2000), pp. 1451–1480.Google Scholar
[10]Goncharov, S. S and Nurtazin, A. T., Constructive models of complete decidable theories, Algebra and Logic, vol. 12 (1973), pp. 67–77.CrossRefGoogle Scholar
[11]Hájek, P., Interpretability and fragments of arithmetic, Arithmetic, Proof Theory, and Computational Complexity (Prague, 1991), Oxford Logic Guides, vol. 23, Oxford University Press, New York, 1993, pp. 185–196.Google Scholar
[12]Hájekand, P.Pudlák, P., Metamathematics of first-order arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998, second printing.Google Scholar
[13]Harizanov, V. S., Turing degrees of certain isomorphic images of computable relations., Annals of Pure and Applid Logic, vol. 93 (1998), pp. 103–113.Google Scholar
[14]Herrmann, E., Infinite chains and antichains in computable partial orderings, this Journal, vol. 66 (2001), pp. 923–934.Google Scholar
[15]Hirschfeldt, D.R., Jockusch, C. G. Jr., Kjos-Hanssen, B., Lempp, S., and Slaman, T.A., Some remarks on the proof-theoretic strength of some combinatorial principles, to appear in the proceedings of the Program on Computational Prospects of Infinity, Singapore 2005.Google Scholar
[16]Hirst, J., Combinatorics in subsystems of second order arithmetic, Ph.D. Dissertation, Pennsylvania State University, 1987.Google Scholar
[17]Jockusch, C.G. Jr., Ramsey's Theorem and recursion theory, this Journal, vol. 37 (1972), pp. 268–280.Google Scholar
[18]Jockusch, C.G. Jr. and Soare, R. I., classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
[19]Jockusch, C.G. Jr. and Stephan, F., A cohesive set which is not high, Mathematical Logic Quarterly, vol. 39 (1993), pp. 515–530, (correction in Mathematical Logic Quarterly vol. 43 (1997), p. 569).CrossRefGoogle Scholar
[20]Lerman, M., On recursive linear orderings, Logic Year 1979–1980 (Lerman, , Schmerl, , and Soare, , editors), Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin, 1981, pp. 132–142.CrossRefGoogle Scholar
[21]Mileti, J. R., Partition theorems and computability theory, Ph.D. Dissertation, University of Illinois at Urbana-Champaign, 2004.Google Scholar
[22]Mourad, J., Fragments of arithmetic and the foundations of the priority method, Ph.D. Dissertation, University of Chicago, 1988.Google Scholar
[23]Paris, J. B., A hierarchy of cuts in models of arithmetic, Model theory of algebra and arithmetic, Lecture Notes in Mathematics, vol. 834, Springer, Berlin-New York, 1980, pp. 312–337.CrossRefGoogle Scholar
[24]Paris, J. B. and Kirby, L. A. S., Σn-collection schemas in arithmetic, Logic Colloquium '77, Studies in Logic and the Foundations of Mathematics, vol. 96, North-Holland, Amsterdam-New York, 1978, pp. 199–209.CrossRefGoogle Scholar
[25]Rosenstein, J. G., Linear orderings, Pure and Applied Mathematics, vol. 98, Academic Press, New York etc, 1982.Google Scholar
[26]Seetapun, D. and Slaman, T. A., On the strength of Ramsey's Theorem, Notre Dame Journal of Formal Logic, vol. 36 (1995), pp. 570–582.CrossRefGoogle Scholar
[27]Simpson, S. G., Degrees of unsolvability: a survey of results, Handbook of mathematical logic (Barwise, , editor), North-Holland, Amsterdam, 1977, pp. 631–652.Google Scholar
[28]Simpson, S. G., Subsystems of second order arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1999.CrossRefGoogle Scholar
[29]Simpson, S. G. and Yu, X., Measure theory and weak König's Lemma, Archive for Mathematical Logic, vol. 30 (1990), pp. 171–180.Google Scholar
[30]Specker, E., Ramsey's Theorem does not hold in recursive set theory, Logic Colloquium '69, Studies in Logic and the Foundations of Mathematics, North-Holland, Amsterdam, 1971.Google Scholar
[31]Szpilrajn, E., Sur l'extension de l'ordre partiel, Fundamenta Mathematicae, vol. 16 (1930), pp. 386–389.CrossRefGoogle Scholar