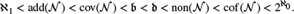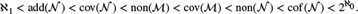Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Goldstern, Martin
and
Klausner, Lukas Daniel
2021.
Cichoń’s diagram and localisation cardinals.
Archive for Mathematical Logic,
Vol. 60,
Issue. 3-4,
p.
343.
Brendle, Jörg
Cardona, Miguel A.
and
Mejía, Diego A.
2021.
Filter-linkedness and its effect on preservation of cardinal characteristics.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 1,
p.
102856.
Goldstern, Martin
Kellner, Jakob
Mejía, Diego A.
and
Shelah, Saharon
2021.
Controlling cardinal characteristics without adding reals.
Journal of Mathematical Logic,
Vol. 21,
Issue. 03,