Compactness and transfer for a fragment of L²

Extract

The language Lⁿ is obtained from the first order predicate calculus by adjoining the quantifier Qⁿ which binds n variables. The formula Qⁿυ₁ … υ_nΨ is given a κ-interpretation for each infinite cardinal κ, namely, “there is a set X of power κ such that Ψx₁ … x_n holds for all distinct x₁ … x_n ϵ X”. L^<ω is the result of adjoining all the Qⁿ quantifiers for each n ϵ ω to the first order predicate calculus.

In [4] we showed that under the assumption 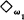(cf. [3]) L^<ω is countably compact under the ω₁-interpretation, and that any sentence σ ϵ L^<ω that has a model in some κ-interpretation where κ is a regular infinite cardinal has a model in the ω₁ interpretation. However, compactness for L^<ω in the κ-interpretation for κ an infinite successor cardinal other than ω₁ and the transfer of satisfiability from ω₁ to any higher power remain open questions under any set theoretic assumptions.

Here we restrict our attention to a small fragment L²⁻ of L² consisting of universal first order formulas along with formulas of the kind Q²υ₁υ₂∀υ₃ … υ_nΨ and ¬Q²υ₁υ₂∀υ₃ … υ_nφ where Ψ and φ are open and no function symbol of arity > 1 occurs in any formula. Assuming the existence of a κ-Souslin tree, this language is λ compact in the κ-interpretation when λ < κ.