Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T06:53:16.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Completeness of global intuitionistic set theory

Published online by Cambridge University Press:  12 March 2014

Satoko Titani
Satoko Titani*
Affiliation:
Department of Mathematics, Chubu University, Kasugai, Aichi 487, Japan, E-mail: titani@isc.chubu.ac.jp
Get access Rights & Permissions [Opens in a new window]

Extract

Gentzen's sequential system LJ of intuitionistic logic has two symbols of implication. One is the logical symbol → and the other is the metalogical symbol ⇒ in sequents

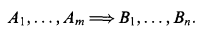
Considering the logical system LJ as a mathematical object, we understand that the logical symbols ∧, ∨, →, ¬, ∀, ∃ are operators on formulas, and ⇒ is a relation. That is, φ ⇒ Ψ is a metalogical sentence which is true or false, on the understanding that our metalogic is a classical logic. In other words, we discuss the logical system LJ in the classical set theory ZFC, in which φ ⇒ Ψ is a sentence.

The aim of this paper is to formulate an intuitionistic set theory together with its metatheory. In Takeuti and Titani [6], we formulated an intuitionistic set theory together with its metatheory based on intuitionistic logic. In this paper we postulate that the metatheory is based on classical logic.

Let Ω be a cHa. Ω can be a truth value set of a model of LJ. Then the logical symbols ∧, ∨, →, ¬, ∀x, ∃x are interpreted as operators on Ω, and the sentence φ ⇒ Ψ is interpreted as 1 (true) or 0 (false). This means that the metalogical symbol ⇒ also can be expressed as a logical operators such that φ ⇒ Ψ is interpreted as 1 or 0.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 2 , June 1997 , pp. 506 - 528
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Grayson, R. J., Heyting valued models for intuitionistic set theory, Applications of sheaves, Lecture Notes in Mathematics, no. 753, Springer-Verlag, Berlin, 1979, Proceedings of the research symposium, Durham, 1977, pp. 402–414.CrossRefGoogle Scholar
[2]Powell, W. C., Extending Gödel's negative interpretation of ZF, this Journal, vol. 40 (1975), pp. 221–229.Google Scholar
[3]Rasiowa, H. and Sikorski, R., Mathematics of metamathematics, 1963.Google Scholar
[4]Takeuti, G., Proof theory, North-Holland, Amsterdam, 1987.Google Scholar
[5]Takeuti, G. and Titani, S., Global intuitionistic fuzzy set theory, The mathematics of fuzzy systems, Tüv-Verlab, Köln, 1985, pp. 291–301.Google Scholar
[6]Takeuti, G. and Titani, S., Globalization of intuitionistic set theory, Annals of Pure and Applied Logic, vol. 33 (1987), pp. 195–211.CrossRefGoogle Scholar