The Complexity of intrinsically r.e. subsets of existentially decidable models

Extract

Recursive model theory involves the study of relationships between recursion theory and model theory. One direction this often takes is to study the effectiveness of various aspects of model theory. This paper examines such questions by examining some properties of recursive models; that is, models whose basic relations, functions, and constants are all uniformly recursive (and whose universe is the set of natural numbers). Somewhat more precisely:

Let 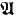be a model whose universe is N, and let (θ(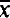))_i be an effective enumeration of all quantifier-free formulas of the language of 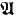. Then 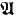is recursive if {〈, i〉: satisfies (θ(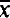))_i, in 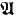} is a recursive subset of N. (Here and throughout the paper, 〈 〉 denotes an effective pairing function, or an effective coding of sequences, as required.) Similarly, let (ϕ(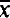))_i be an effective enumeration of all existential formulas of the language of 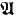. Then 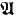is existentially decidable if {〈, i〉: satisfies (ϕ(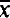))_i in 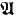} is a recursive subset of N.

It is clear that if 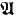is recursive and 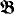is a model isomorphic to 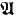, then 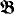may lose many of the recursive properties of 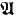. In the simplest example, 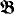could easily fail to be a recursive model. But even if we require that 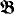be a recursive model, it could still fail to retain other recursive properties of 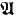. An example of the sort of property which can be studied in this vein is the following notion, introduced by Ash and Nerode in [2].