Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-13T07:18:12.115Z Has data issue: false hasContentIssue false
  • English
  • Français

THE COMPLEXITY OF THE EMBEDDABILITY RELATION BETWEEN TORSION-FREE ABELIAN GROUPS OF UNCOUNTABLE SIZE

Published online by Cambridge University Press:  01 August 2018

FILIPPO CALDERONI
FILIPPO CALDERONI*
Affiliation:
DIPARTIMENTO DI MATEMATICA «GIUSEPPE PEANO» UNIVERSITÀ DI TORINO VIA CARLO ALBERTO 10, 10123 TORINO, ITALYE-mail:filippo.calderoni@unito.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for every uncountable cardinal κ such that κ<κ = κ, the quasi-order of embeddability on the κ-space of κ-sized graphs Borel reduces to the embeddability on the κ-space of κ-sized torsion-free abelian groups. Then we use the same techniques to prove that the former Borel reduces to the embeddability relation on the κ-space of κ-sized R-modules, for every $\mathbb{S}$-cotorsion-free ring R of cardinality less than the continuum. As a consequence we get that all the previous are complete 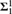$\Sigma _1^1$ quasi-orders.

Keywords

03E1520K2020K40Borel reducibilitytorsion-free abelian groupsgeneralized descriptive set theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 2 , June 2018 , pp. 703 - 716
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andretta, A. and Ros, L. M., Classifying uncountable structures up to bi-embeddability, preprint, 2016, arXiv:1609.09292v1.Google Scholar
Baer, R., Abelian groups without elements of finite order. Duke Mathematical Journal, vol. 3 (1937), no. 1, pp. 68–122.CrossRefGoogle Scholar
Calderoni, F., Mildenberger, H., and Ros, L. M., Uncountable structures are not classifiable up to bi-embeddability, submitted.Google Scholar
Calderoni, F. and Thomas, S., The bi-embeddability relation for countable abelian groups. Transactions of the American Mathematical Society, to appear.Google Scholar
Corner, A. L. S., Every countable reduced torsion-free ring is an endomorphism ring. Proceedings of the London Mathematical Society. Third Series, vol. 13 (1963), pp. 687–710.CrossRefGoogle Scholar
Downey, R. and Montalbán, A., The isomorphism problem for torsion-free abelian groups is analytic complete. Journal of Algebra, vol. 320 (2008), no. 6, pp. 2291–2300.CrossRefGoogle Scholar
Friedman, S.-D., Hyttinen, T., and Kulikov, V., Generalized descriptive set theory and classification theory. Memoirs of the American Mathematical Society, vol. 230 (2014), no. 1081, pp. vi+80.Google Scholar
Fuchs, L., Infinite Abelian Groups. Vol. I, Pure and Applied Mathematics, vol. 36, Academic Press, New York, London, 1970.Google Scholar
Fuchs, L., Abelian Groups, Springer Monographs in Mathematics, Springer, Cham, 2015.CrossRefGoogle Scholar
Göbel, R. and Przeździecki, A. J., An axiomatic construction of an almost full embedding of the category of graphs into the category of R-objects. Journal of Pure and Applied Algebra, vol. 218 (2014), no. 2, pp. 208–217.CrossRefGoogle Scholar
Göbel, R. and Trlifaj, J., Approximations and Endomorphism Algebras of Modules. Volume 2, extended ed., de Gruyter Expositions in Mathematics, vol. 41, Walter de Gruyter GmbH & Co. KG, Berlin, 2012, Predictions.CrossRefGoogle Scholar
Hjorth, G., The isomorphism relation on countable torsion free abelian groups. Fundamenta Mathematicae, vol. 175 (2002), no. 3, pp. 241–257.CrossRefGoogle Scholar
Hyttinen, T. and Kulikov, V., On ${\rm{\Sigma }}_1^1$-complete equivalence relations on the generalized Baire space. Mathematical Logic Quarterly, vol. 61 (2015), no. 1–2, pp. 66–81.CrossRefGoogle Scholar
Hyttinen, T. and Moreno, M., On the reducibility of isomorphism relations. Mathematical Logic Quarterly, vol. 63 (2017), no. 3–4, pp. 175–192.CrossRefGoogle Scholar
Kechris, A. S., Classical Descriptive Set Theory, Graduate Texts in Mathematics, vol. 156, Springer-Verlag, New York, 1995.CrossRefGoogle Scholar
Louveau, A. and Rosendal, C., Complete analytic equivalence relations. Transactions of the American Mathematical Society, vol. 357 (2005), no. 12, pp. 4839–4866.CrossRefGoogle Scholar
Ros, L. M., The descriptive set-theoretical complexity of the embeddability relation on models of large size. Annals of Pure and Applied Logic, vol. 164 (2013), no. 12, pp. 1454–1492.Google Scholar
Przeździecki, A. J., An almost full embedding of the category of graphs into the category of abelian groups. Advances in Mathematics, vol. 257 (2014), pp. 527–545.CrossRefGoogle Scholar
Rotman, J. J., An Introduction to Homological Algebra, second ed., Universitext, Springer, New York, 2009.CrossRefGoogle Scholar
Thomas, S., The classification problem for torsion-free abelian groups of finite rank. Journal of the American Mathematical Society, vol. 16 (2003), no. 1, pp. 233–258.CrossRefGoogle Scholar
Williams, J., Universal countable Borel quasi-orders, this Journal, vol. 79 (2014), no. 3, pp. 928–954.Google Scholar