Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T06:45:06.147Z Has data issue: false hasContentIssue false
  • English
  • Français

The complexity of the modal predicate logic of “true in every transitive model of ZF”

Published online by Cambridge University Press:  12 March 2014

Vann McGee
Vann McGee*
Affiliation:
Department of Linguistics and Philosophy, Massachusetts Institute of Technology, Cambridge, MA 02139, USA E-mail: vmcgee@mit.edu
Get access Rights & Permissions [Opens in a new window]

Extract

Robert Solovay [8] investigated the version of the modal sentential calculus one gets by taking “□ϕ” to mean “ϕ is true in every transitive model of Zermelo-Fraenkel set theory (ZF).” Defining an interpretation to be a function * taking formulas of the modal sentential calculus to sentences of the language of set theory that commutes with the Boolean connectives and sets (□ϕ)* equal to the statement that ϕ* is true in every transitive model of ZF, and stipulating that a modal formula ϕ is valid if and only if, for every interpretation *, ϕ* is true in every transitive model of ZF, Solovay obtained a complete and decidable set of axioms.

In this paper, we stifle the hope that we might continue Solovay's program by getting an analogous set of axioms for the modal predicate calculus. The set of valid formulas of the modal predicate calculus is not axiomatizable; indeed, it is complete .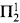

We also look at a variant notion of validity according to which a formula ϕ counts as valid if and only if, for every interpretation *, ϕ* is true. For this alternative conception of validity, we shall obtain a lower bound of complexity: every set which is 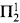in the set of sentences of the language of set theory true in the constructible universe will be 1-reducible to the set of valid modal formulas.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 4 , December 1997 , pp. 1371 - 1378
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Artemov, Sergei, Nonarithmeticity of truth predicate logics of provability, Doklady Akademeii nauk SSSR, vol. 284 (1985), pp. 270–71, English translation in Soviet Mathematics—Doklady, vol. 32 (1986), pp. 403–5.Google Scholar
[2]Barwise, Jon, Admissible sets and structures, Springer-Verlag, Berlin, Heidelberg, and New York, 1975.CrossRefGoogle Scholar
[3]Boolos, George, The logic of provability, Cambridge University Press, Cambridge and New York, 1993.Google Scholar
[4]Boolos, George and McGee, Vann, The degree of the set of sentences of predicate provability logic that are true under every interpretation, this Journal, vol. 52 (1987), pp. 165–71.Google Scholar
[5]Jech, Thomas, Set theory, Academic Press, New York, San Francisco, and London, 1978.Google Scholar
[6]McGee, Vann, On the degrees of unsolvability of modal predicate logics of provability, this Journal, vol. 59 (1994), pp. 253–61.Google Scholar
[7]Quine, Willard Van Orman, Mathematical logic, 2nd ed., Harper and Row, New York, 1951.CrossRefGoogle Scholar
[8]Solovay, Robert, Provability interpretations of modal logic, Israel Journal of Mathematics, vol. 25 (1976), pp. 287–304.CrossRefGoogle Scholar
[9]Vardanyan, V A., Arithmetical complexity of predicate logics of provability and their fragments, Doklady Akademeii nauk SSSR, vol. 288 (1986), pp. 11–14.Google Scholar