Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T18:44:54.506Z Has data issue: false hasContentIssue false
  • English
  • Français

THE COMPUTATIONAL CONTENT OF INTRINSIC DENSITY

Published online by Cambridge University Press:  01 August 2018

ERIC P. ASTOR
ERIC P. ASTOR*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CONNECTICUT 341 MANSFIELD RD U-1009 STORRS, CT 06269-1009, USAE-mail:eric.astor@uconn.eduURL: http://www.math.uconn.edu/∼astor
Get access Rights & Permissions [Opens in a new window]

Abstract

In a previous article, the author introduced the idea of intrinsic density—a restriction of asymptotic density to sets whose density is invariant under computable permutation. We prove that sets with well-defined intrinsic density (and particularly intrinsic density 0) exist only in Turing degrees that are either high (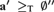${\bf{a}}\prime { \ge _{\rm{T}}}\emptyset \prime \prime$) or compute a diagonally noncomputable function. By contrast, a classic construction of an immune set in every noncomputable degree actually yields a set with intrinsic lower density 0 in every noncomputable degree.

We also show that the former result holds in the sense of reverse mathematics, in that (over RCA0) the existence of a dominating or diagonally noncomputable function is equivalent to the existence of a set with intrinsic density 0.

Keywords

03D28intrinsic densityTuring degreesreverse mathematics
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 2 , June 2018 , pp. 817 - 828
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Astor, E. P., Asymptotic density, immunity and randomness. Computability, vol. 4 (2015), no. 2, pp. 141–158.CrossRefGoogle Scholar
Astor, E. P., Hirschfeldt, D. R., and Jockusch, C. G. Jr., Dense computability, upper cones, and minimal pairs, in preparation.Google Scholar
Downey, R. G. and Hirschfeldt, D. R., Algorithmic Randomness and Complexity, Theory and Applications of Computability, Springer-Verlag, New York, 2010.CrossRefGoogle Scholar
Downey, R. G., Jockusch, C. G. Jr., McNicholl, T. H., and Schupp, P. E., Asymptotic density and the Ershov hierarchy. Mathematical Logic Quarterly, vol. 61 (2015), no. 3, pp. 189–195.CrossRefGoogle Scholar
Downey, R. G., Jockusch, C. G. Jr., and Schupp, P. E., Asymptotic density and computably enumerable sets. Journal of Mathematical Logic, vol. 13 (2013), no. 02.CrossRefGoogle Scholar
Dzhafarov, D. D. and Igusa, G., Notions of robust information coding. Computability, vol. 6 (2017), no. 2, pp. 105–124.CrossRefGoogle Scholar
Hirschfeldt, D. R., Jockusch, C. G. Jr., Kuyper, R., and Schupp, P. E., Coarse reducibility and algorithmic randomness, this Journal, vol. 81 (2016), no. 3, pp. 1028–1046.Google Scholar
Hirschfeldt, D. R., Jockusch, C. G. Jr., McNicholl, T. H., and Schupp, P. E., Asymptotic density and the coarse computability bound. Computability, vol. 5 (2016), no. 1, pp. 13–27.CrossRefGoogle Scholar
Hölzl, R., Raghavan, D., Stephan, F., and Zhang, J., Weakly represented families in reverse mathematics, Computability and Complexity: Essays Dedicated to Rodney G. Downey on the Occasion of his 60th Birthday(Day, A., Fellows, M., Greenberg, N., Khoussainov, B., Melnikov, A., and Rosamond, F., editors), Springer International Publishing, Cham, Switzerland, 2017, pp. 160–187.CrossRefGoogle Scholar
Igusa, G., Nonexistence of minimal pairs for generic computability, this Journal, vol. 78 (2013), no. 2, pp. 511–522.Google Scholar
Jockusch, C. G. Jr., Upward closure and cohesive degrees. Israel Journal of Mathematics, vol. 15 (1973), no. 3, pp. 332–335.CrossRefGoogle Scholar
Jockusch, C. G. Jr. and Schupp, P. E., Generic computability, Turing degrees, and asymptotic density. Journal of the London Mathematical Society, vol. 85 (2012), no. 2, pp. 472–490.CrossRefGoogle Scholar
Jockusch, C. G. Jr. and Stephan, F., A cohesive set which is not high. Mathematical Logic Quarterly, vol. 39 (1993), no. 1, pp. 515–530.CrossRefGoogle Scholar
Kapovich, I., Myasnikov, A., Schupp, P. E., and Shpilrain, V., Generic-case complexity, decision problems in group theory, and random walks. Journal of Algebra, vol. 264 (2003), no. 2, pp. 665–694.CrossRefGoogle Scholar
Kjos-Hanssen, B., Merkle, W., and Stephan, F., Kolmogorov complexity and the Recursion Theorem. Transactions of the American Mathematical Society, vol. 363 (2011), no. 10, pp. 5465–5480.CrossRefGoogle Scholar
Martin, D. A., Classes of recursively enumerable sets and degrees of unsolvability. Mathematical Logic Quarterly, vol. 12 (1966), no. 1, pp. 295–310.CrossRefGoogle Scholar
Miller, J. S. and Nies, A., Randomness and computability: Open questions. The Bulletin of Symbolic Logic, vol. 12 (2006), no. 3, pp. 390–410.CrossRefGoogle Scholar
Nies, A., Stephan, F., and Terwijn, S. A., Randomness, relativization, and turing degrees, this Journal, vol. 70 (2005), no. 2, pp. 515–535.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, Perspectives in Logic, Cambridge University Press, New York, 2009.CrossRefGoogle Scholar
Soare, R. I., Turing Computability: Theory and Applications, Theory and Applications of Computability, Springer-Verlag, Berlin, 2016.CrossRefGoogle Scholar