Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Halbeisen, Lorenz
and
Shelah, Saharon
2001.
Relations Between Some Cardinals in the Absence of the Axiom of Choice.
Bulletin of Symbolic Logic,
Vol. 7,
Issue. 2,
p.
237.
Halbeisen, Lorenz J.
2012.
Combinatorial Set Theory.
p.
157.
Halbeisen, Lorenz J.
2012.
Combinatorial Set Theory.
p.
71.
Yegnanarayanan, Venkataraman
and
Parthiban, Angamuthu
2013.
Chromatic Number of Graphs with Special Distance Sets-V.
Open Journal of Discrete Mathematics,
Vol. 03,
Issue. 01,
p.
1.
Vejjajiva, Pimpen
and
Panasawatwong, Supakun
2014.
A Note on Weakly Dedekind Finite Sets.
Notre Dame Journal of Formal Logic,
Vol. 55,
Issue. 3,
2014.
Set Theoretical Aspects of Real Analysis.
p.
411.
Keremedis, Kyriakos
2016.
Non‐discrete metrics in and some notions of finiteness.
Mathematical Logic Quarterly,
Vol. 62,
Issue. 4-5,
p.
383.
Halbeisen, Lorenz J.
2017.
Combinatorial Set Theory.
p.
191.
Halbeisen, Lorenz J.
2017.
Combinatorial Set Theory.
p.
103.
Shen, Guozhen
2017.
Generalizations of Cantor's theorem in .
Mathematical Logic Quarterly,
Vol. 63,
Issue. 5,
p.
428.
Aksornthong, Navin
and
Vejjajiva, Pimpen
2018.
Relations between cardinalities of the finite sequences and the finite subsets of a set.
Mathematical Logic Quarterly,
Vol. 64,
Issue. 6,
p.
529.
Halbeisen, Lorenz
2018.
A weird relation between two cardinals.
Archive for Mathematical Logic,
Vol. 57,
Issue. 5-6,
p.
593.
Tachtsis, E.
2019.
On the existence of permutations of infinite sets without fixed points in set theory without choice.
Acta Mathematica Hungarica,
Vol. 157,
Issue. 2,
p.
281.
Sonpanow, Nattapon
and
Vejjajiva, Pimpen
2019.
Factorials and the finite sequences of sets.
Mathematical Logic Quarterly,
Vol. 65,
Issue. 1,
p.
116.
Shen, Guozhen
2020.
A Note on Strongly Almost Disjoint Families.
Notre Dame Journal of Formal Logic,
Vol. 61,
Issue. 2,
Nuntasri, Jukkrid
Panasawatwong, Supakun
and
Vejjajiva, Pimpen
2021.
The finite subsets and the permutations with finitely many non‐fixed points of a set.
Mathematical Logic Quarterly,
Vol. 67,
Issue. 2,
p.
258.
Lisica, Ju.T.
2023.
On one of Specker's theorems.
Topology and its Applications,
Vol. 329,
Issue. ,
p.
108383.
Halbeisen, Lorenz
Plati, Riccardo
Schumacher, Salome
and
Shelah, Saharon
2023.
Four cardinals and their relations in ZF.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 2,
p.
103200.
Shen, Guozhen
2023.
The power set and the set of permutations with finitely many non‐fixed points of a set.
Mathematical Logic Quarterly,
Vol. 69,
Issue. 1,
p.
40.
Phansamdaeng, Palagorn
and
Vejjajiva, Pimpen
2023.
The cardinality of the partitions of a set in the absence of the Axiom of Choice.
Logic Journal of the IGPL,
Vol. 31,
Issue. 6,
p.
1225.
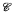 and
and 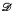 , either
, either 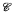 ≤
≤ 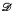 or
or 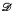 ≤
≤ 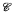 . However, in ZF this is no longer so. For a given infinite set A consider seq1-1(A), the set of all sequences of A without repetition. We compare |seq1-1(A)|, the cardinality of this set, to |
. However, in ZF this is no longer so. For a given infinite set A consider seq1-1(A), the set of all sequences of A without repetition. We compare |seq1-1(A)|, the cardinality of this set, to |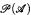 |, the cardinality of the power set of A. What is provable about these two cardinals in ZF? The main result of this paper is that ZF ⊢ ∀A(| seq1-1(A)| ≠ |
|, the cardinality of the power set of A. What is provable about these two cardinals in ZF? The main result of this paper is that ZF ⊢ ∀A(| seq1-1(A)| ≠ |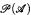 |), and we show that this is the best possible result. Furthermore, it is provable in ZF that if B is an infinite set, then | fin(B)| < |
|), and we show that this is the best possible result. Furthermore, it is provable in ZF that if B is an infinite set, then | fin(B)| < | 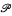 (B*)| even though the existence for some infinite set B* of a function ƒ from fin(B*) onto
(B*)| even though the existence for some infinite set B* of a function ƒ from fin(B*) onto 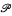 (B*) is consistent with ZF.
(B*) is consistent with ZF.
