Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T19:25:07.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Consistency of Suslin's hypothesis, a nonspecial Aronszajn tree, and GCH

Published online by Cambridge University Press:  12 March 2014

Chaz Schlindwein
Chaz Schlindwein*
Affiliation:
Department of Mathematics, Pennsylvania State University, University Park, Pennsylvania 18602,, E-mail:chaz@helios.nevada.edu
*
Dept. of Mathematical Sciences, University of Nevadaat Las Vegas Las Vegas, Nevada 89154
Get access Rights & Permissions [Opens in a new window]

Extract

Introduction. In [Sh, Chapter IX], Shelah constructs a model of set theory in which Suslin's hypothesis is true, yet there is an Aronszajn tree which is not special. In his model, we have 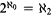. He asks whether the same result could be obtained consistently with CH. In this paper, we answer his question in the affirmative.

Let us say that a tree T is S-st-special iff there is a function ƒ with dom(f) = {t ∈ T: rank(t) ∈ S} and for every t1 < t2 both in dom(t) we have f(t2) ≠ f(t1) < rank(t1). In Shelah's model, every tree is S-st-special for some fixed stationary costationary set S. Also, there is some tree T such that T is not S′-st-special whenever S′ – S is stationary. These properties, which are sufficient to ensure that Suslin's hypothesis holds and that T is not special, also hold in the model constructed in this paper. These properties also ensure that every Aronszajn tree has a stationary antichain (i.e., an antichain A such that {rank(t): t ∈ A} is stationary). Hence, it is natural to ask whether there is a model of Suslin's hypothesis in which some Aronszajn tree has no stationary antichain. We answer in the affirmative in [S].

The construction we use owes much to Shelah's approach to the theorem, due to Jensen (see [DJ]), that CH is consistent with Suslin's hypothesis. This is given in [Sh, Chapter V].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 1 , March 1994 , pp. 1 - 29
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ba] Baumgartner, James, Iterated Forcing, Surveys in set theory (Mathias, A.R.D., editor), London Mathematical Society Lecture Note Series, vol. 87, Cambridge University Press, London and New York, 1983, pp. 1–59.Google Scholar
[BMR] Baumgartner, J. E., Malitz, J. I., and Reinhardt, W., Embedding trees in the rationals, Proceedings of the National Academy of Sciences of the United States of America, vol. 67 (1970), pp. 1748–1753.Google ScholarPubMed
[DJ] Devlin, K. J. and Johnsbråten, H., The Souslin problem, Lecture Notes in Mathematics, vol. 405, Springer-Verlag, Berlin and New York, 1974.CrossRefGoogle Scholar
[F] Friedman, H., On closed sets of ordinals, Proceedings of the American Math. Society, vol. 43 (1974), pp. 190–192.CrossRefGoogle Scholar
[J] Jech, T. J., Multiple forcing, Cambridge University Press, London and New York, 1986.Google Scholar
[JJ] Jensen, R. B. and Johnsbråten, H., A new construction of a nonconstructible subset of ω, Fundamenta Mathematical vol. 81 (1974), pp. 279–290.Google Scholar
[K] Kunen, K., Set theory, An introduction to independence proofs, North-Holland, Amsterdam, 1980.Google Scholar
[S2] Schlindwein, C., Suslin's hypothesis does not imply stationary antichains, Annals of Pure and Applied Logic, vol. 64 (1993), pp. 153–167.Google Scholar
[S3] Schlindwein, C., Simplified RCS iterations, Archive for Mathematical Logic, vol. 32 (1993), pp. 341–349.CrossRefGoogle Scholar
[S89] Schlindwein, C., Special nonspecial ℵ1-trees, Set theory and its applications (J. Steprans and S. Watson, editors) Lecture Notes in Mathematics, vol. 1041, Springer-Verlag, Berlin and New York, 1989, pp. 160–166.Google Scholar
[Sh] Shelah, S., Proper forcing, Lecture Notes in Mathematics, vol. 940, Springer-Verlag, Berlin and New York, 1982.CrossRefGoogle Scholar