Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T17:57:44.214Z Has data issue: false hasContentIssue false
  • English
  • Français

The consistency of ZFC + 2ℵ0 > ℵω + ℐ(ℵ2) = ℐ(ℵω)

Published online by Cambridge University Press:  12 March 2014

Martin Gilchrist  and
Saharon Shelah
Martin Gilchrist
Affiliation:
Simon Fraser University, Burnaby, British Columbia, Canada, E-mail: gilchris@cs.sfu.ca
Saharon Shelah
Affiliation:
Mathematics Institute, Hebrew University of Jerusalem, Givat Ram, 91904 Jerusalem, Israel, E-mail: shelah@math.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Extract

Let κ be an uncountable cardinal and the edges of a complete graph with κ vertices be colored with ℵ0 colors. For 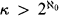the Erdős-Rado theorem implies that there is an infinite monochromatic subgraph. However, if 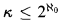, then it may be impossible to find a monochromatic triangle. This paper is concerned with the latter situation. We consider the types of colorings of finite subgraphs that must occur when 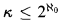. In particular, we are concerned with the case ℵ1 ≤ κ ≤ ℵω.

The study of these color patterns (known as identities) has a history that involves the existence of compactness theorems for two cardinal models [4]. When the graph being colored has size ℵ1, the identities that must occur (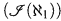(ℵ1)) have been classified by Shelah [6]. If the graph has size greater than or equal to ℵω the identities that must occur (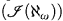(ℵω)) have also been classified in [5]. This leaves open the question of how the sets 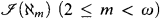(ℵm) (2 ≤ m < ω) fit between 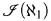(ℵ1) and ⊆ 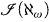(ℵω). Some progress in this direction has been made in the paper [2]. It is there shown that if ZFC is consistent then so is 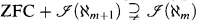for each m < ω. The number of colors is fixed at ℵ0 as it is the natural place to start and the results here can be generalized to more colors. We first give some definitions and establish some notation.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 4 , December 1997 , pp. 1151 - 1160
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Erdős, P., Partition relation on cardinals, Acta Mathematica Hungarica, vol. 16 (1965), pp. 93–196.Google Scholar
[2]Gilchrist, M. and Shelah, S, Identities on cardinals less than ℵω, submitted.Google Scholar
[3]Jech, T., Multiple forcing, Cambridge University Press, 1986.Google Scholar
[4]Schmerl, J., Transfer theorems and their applications to logics, Model theoretic logics, 1985, pp. 177–209.Google Scholar
[5]Shelah, S., A two cardinal theorem and a combinatorial theorem, Proceedings of the American Mathematical Society, vol. 62 (1977), no. 1, pp. 134–136.CrossRefGoogle Scholar
[6]Shelah, S., Appendix to models with second order properties II, Annals of Mathematical Logic, vol. 14 (1978), pp. 223–226.CrossRefGoogle Scholar
[7]Shelah, S., Models with second order properties II, Annals of Mathematical Logic, vol. 14 (1978), pp. 73–87.CrossRefGoogle Scholar
[8]Williams, N., Combinatorial set theory, North Holland, 1977.Google Scholar