Article contents
The consistency strength of choiceless failures of SCH
Published online by Cambridge University Press: 12 March 2014
Abstract
We determine exact consistency strengths for various failures of the Singular Cardinals Hypothesis (SCH) in the setting of the Zermelo-Fraenkel axiom system ZF without the Axiom of Choice (AC). By the new notion of parallel Prikry forcing that we introduce, we obtain surjective failures of SCH using only one measurable cardinal, including a surjective failure of Shelah's pcf theorem about the size of the power set of ℵω. Using symmetric collapses to ℵω, 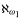 , or
, or 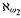 , we show that injective failures at ℵω,
, we show that injective failures at ℵω, 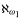 , or
, or 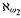 can have relatively mild consistency strengths in terms of Mitchell orders of measurable cardinals. Injective failures of both the aforementioned theorem of Shelah and Silver's theorem that GCH cannot first fail at a singular strong limit cardinal of uncountable cofinality are also obtained. Lower bounds are shown by core model techniques and methods due to Gitik and Mitchell.
can have relatively mild consistency strengths in terms of Mitchell orders of measurable cardinals. Injective failures of both the aforementioned theorem of Shelah and Silver's theorem that GCH cannot first fail at a singular strong limit cardinal of uncountable cofinality are also obtained. Lower bounds are shown by core model techniques and methods due to Gitik and Mitchell.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2010
References
REFERENCES
- 2
- Cited by

