Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T17:39:14.771Z Has data issue: false hasContentIssue false
  • English
  • Français

A constructive analysis of RM

Published online by Cambridge University Press:  12 March 2014

Arnon Avron
Arnon Avron*
Affiliation:
Department of Mathematical Sciences, University of Tel-Aviv, Ramat-Aviv, Tel-Aviv, Israel
*
Laboratory for Foundations of Computer Sciences, University of Edinburgh, Edinburgh EH9 3JZ, Scotland
Get access Rights & Permissions [Opens in a new window]

Extract

The system RM is the most well-understood (and to our opinion, also the most important) system among the logics developed by the Anderson and Belnap school. In this paper we investigate RM from a constructive point of view. For example, we give a new proof of the completeness of RM relative to the Sugihara matrix (first shown by Meyer), a proof in which a p.r. procedure is presented, applying which to a sentence A in RM language yields either a proof of it in RM or a refuting valuation for it in the Sugihara matrix SZ.

Two topics dealt with in this work deserve a special attention.

a) The admissibility of γ. This is a famous theorem of Meyer and Dunn. In [1] Anderson and Belnap emphasize that “the Meyer-Dunn argument … guarantees the existence of a proof of B, but there is no guarantee that the proof of B is related in any sort of plausible way to the proofs of A and Ā ∨ B.” In §2 we provide such a guarantee for the RM-case. In fact, we give there a direct method of obtaining a proof of B from given proofs of A and Ā ∨ B.

b) The relationships betweenRMand its full negation-implication fragment. RM is known ([1, pp. 148–149], and [3]) to be a conservative extension of 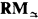(Sobociński 3-valued logic; see [4]). Anderson and Belnap admit [1, p. 149] that this fact came to them as a distinct surprise, since RM as a whole is far from being three-valued. In this paper, however, this “surprising” fact appears quite natural (see III.3). In fact, we show that 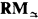, is the “hard core” of RM, since our proof of the completeness of RM is based in an essential way on the completeness of 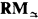relative to the Sobociński matrix, and since the Gentzen-type calculus we develop for RM is a direct extension of a similar (but much simpler) calculus for 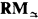. Because of the importance 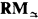has in this work, we devote the first section to a constructive investigation of it.

We note, finally, that the Gentzen-type calculus mentioned above admits cut-elimination and normal-form techniques. (Such calculi were found till now only for RM without distribution.)

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 52 , Issue 4 , December 1987 , pp. 939 - 951
Copyright
Copyright © Association for Symbolic Logic 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Anderson, A. R. and Belnap, N. D., Entailment. Vol. 1, Princeton University Press, Princeton, New Jersey, 1975.Google Scholar
[2]Avron, A., Relevant entailment—semantics and formal systems, this Journal, vol. 49 (1984), pp. 334–342.Google Scholar
[3]Parks, R. Z., A note on R-mingle and Sobocinski's three-valued logic, Notre Dame Journal of Formal Logic, vol. 13 (1972), pp. 227–228.CrossRefGoogle Scholar
[4]Sobociński, B., Axiomatization of a partial system of three-valued calculus of propositions, Journal of Computing Systems, vol. 1 (1952), pp. 23–55.Google Scholar
[5]Pottinoer, G., Uniform, cut-free formulations of T, S4 and S5, this Journal, vol. 48 (1983), p. 900 (abstract).Google Scholar