Correction to ‘A model theoretic characterisation of effective operations’

Extract

With the definition of effective operations as stated in the paper cited above (this Journal, vol. 35 (1970), p. 217), the last step of Lemma 1 does not appear to extend to types ≥ 3. This may be rectified by altering the second clause of the definition of effective operation (loc. cit. p. 217) to read:

ℱ is an effective operation of type i + 2 with Gödel number f∈E _i+2, if for every g∈E _i+1 there is an effective operation 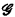of type i + 1 (not depending on ℱ and f) with Gödel number g such that ℱ(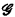) = p(f, g).

With this definition the proofs go through without alteration.

There are two other variants for representing an effective operation by higher type objects.

I. We adopt the definition of effective as given in the text, and require the terms 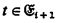to satisfy the additional condition

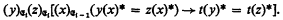
II. Here we add to the definition of effective operations given in the text the condition:

If ℱ and ℱ₁ are effective operations of type i + 2 and 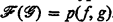for all effective operations 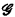of type i + 1, then ℱ = ℱ₁.

We now require terms s, t ∈ f_i to satisfy the additional condition

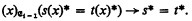
The proof of Lemmas 1 and 2 are easily modified to establish I and II.

Perhaps II may be regarded as giving the most natural characterisation since in this case all terms represent continuous functionals.