Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T17:39:37.687Z Has data issue: false hasContentIssue false
  • English
  • Français

Countable homogeneous relational structures and ℵ0-categorical theories

Published online by Cambridge University Press:  12 March 2014

C. Ward Henson
C. Ward Henson*
Affiliation:
Duke University, Durham, North Carolina 27706
Get access Rights & Permissions [Opens in a new window]

Extract

A relational structure 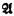of cardinality ℵ0 is called homogeneous by Fraissé [1] if each isomorphism between finite substructures of 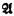can be extended to an automorphism of 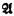. In §1 of this paper it is shown that there are 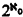isomorphism types of such structures for the first order language L0 with a single (binary) relation symbol, answering a question raised by Fraissé. In fact, as is shown in §2, a family of 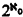nonisomorphic homogeneous structures for L0 can be constructed, each member 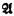of which satisfies the following conditions (where U is the homogeneous, ℵ0-universal graph, the structure of which is considered in [4]):

(i) The relation R of 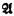is asymmetric (R ∩ R−1 = ∅);

(ii) If A is the domain of 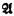and S is the symmetric relation R ∪ R−1, then (A, S) is isomorphic to U. That is, each 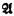may be regarded as the result of assigning a unique direction to each edge of the graph U.

Let T0 be the first order theory of all homogeneous structures for L0 which have cardinality ℵ0. In §3 (which can be read independently of §2) it is shown that T0 has 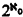complete extensions (in L0), each of which is ℵ0-categorical. Moreover, among the complete extensions of T0 are theories of arbitrary (preassigned) degree of unsolvability. In particular, there exists an undecidable, ℵ0-categorieal theory in L0, which answers a question raised by Grzegorczyk [2], [3].

It follows from Theorem 6 of [3] that there are ℵ0-categorical theories of partial orderings which have arbitrarily high degrees of unsolvability. This is in sharp contrast to the situation for linear orderings, which were the motivation for Fraissé's early work. Indeed, as is shown in [10], every ℵ0-categorical theory of a linear ordering is finitely axiomatizable. (W. Glassmire [12] has independently shown the existence of 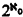theories in L0 which are all ℵ0-categorical, and C. Ash [13] has independently shown that such theories exist with arbitrary degree of unsolvability.)

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 37 , Issue 3 , September 1972 , pp. 494 - 500
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Fraissé, Roland, Sur l'extension aux relations de quelques proprietés des ordres, Annales Scientifiques l'École Normale Supérieure, vol. 71 (1954), pp. 361–388.CrossRefGoogle Scholar
[2]Grzegorczyk, Andrzej, Logical uniformity by decomposition and categoricity in ℵ0, Bulletin de l'Académie Polonaise des Sciences, Série Sciences, Mathematiques, Astronomiques et Physiques, vol. 16 (1968), pp. 687–692.Google Scholar
[3]Grzegorczyk, Andrzej, Decision procedures for theories categorical in ℵ0Symposium on automatic demonstration, Lecture Notes in Mathematics, No. 125, Springer-Verlag, Berlin, 1970, pp. 87–100.CrossRefGoogle Scholar
[4]Henson, C. Ward, A family of countable homogeneous graphs, Pacific Journal of Mathematics, vol. 38 (1971), pp. 69–83.CrossRefGoogle Scholar
[5]Jónsson, Bjarni, Universal relational systems, Mathematica Scandinaviea, vol. 4 (1956), pp. 193–208.CrossRefGoogle Scholar
[6]Jónsson, Bjarni, Homogeneous universal relational systems, Mathematica Scandinaviea, vol. 8 (1960), pp. 137–142.CrossRefGoogle Scholar
[7]Morley, Michael and Vaught, Robert, Homogeneous universal models, Mathematica Scandinaviea, vol. 11 (1962), pp. 37–57.CrossRefGoogle Scholar
[8]Rado, Richard, Universal graphs and universal functions, Acta Arithmetica, vol. 9 (1964), pp. 331–340.CrossRefGoogle Scholar
[9]Rado, Richard, Universal graphs, A seminar in graph theory (Harary, F., editor) Holt, Rinehart and Winston, New York, 1967, pp. 83–85.Google Scholar
[10]Rosenstein, Joseph G., ℵ0-categoricity of linear orderings, Fundamenta Mathematicae, vol. 64 (1969), pp. 1–5.CrossRefGoogle Scholar
[11]Shoenfield, Joseph, Mathematical logic, Addison-Wesley, Reading, Mass., 1969.Google Scholar
[12]Glassmire, William, A problem in categoricity, Notices of the American Mathematical Society, vol. 17 (1970), p. 295, Abstract #70T-E7.Google Scholar
[13]Ash, Christopher, Undecidable ℵ0-categorical theories, Notices of the American Mathematical Society, vol. 18 (1971), p. 423, Abstract #71T-E10.Google Scholar