Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T07:13:42.499Z Has data issue: false hasContentIssue false
  • English
  • Français

Creativeness and completeness in recursion categories of partial recursive operators

Published online by Cambridge University Press:  12 March 2014

Franco Montagna  and
Andrea Sorbi
Franco Montagna
Affiliation:
Dipartimento di Matematica, Università di Siena, 53100 Siena, Italy
Andrea Sorbi
Affiliation:
Dipartimento di Matematica, Università di Siena, 53100 Siena, Italy
Get access Rights & Permissions [Opens in a new window]

Extract

Recursion categories have been proposed by Di Paola and Heller in [DPH] as the basis for a category-theoretic approach to recursion theory, in the context of a more general and ambitious project of a purely algebraic treatment of incompleteness phenomena. The way in which the classical notion of creative set is rendered in this new category-theoretic framework plays, therefore, a central role. This is done in [DPH] (Definition 8.1) by defining the notion of creative domains or, rather, domains which are creative relative to some criterion: thus, in a recursion category, every criterion provides a notion of creativeness.

A basic result on creative domains (cf. [DPH, Theorem 8.13]) is that, under certain assumptions, a version of the classical result, due to Myhill [MYH], stating that every creative set is complete, holds: in a recursion category with equality (i.e. 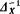exists for every object X) and having enough atoms, every domain which is creative with respect to atoms is also complete.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 3 , September 1989 , pp. 1023 - 1041
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[DKM]Dekker, J. C. E. and Myhill, J., Some thoerems on classes of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 81 (1958), pp. 25–59.CrossRefGoogle Scholar
[DPH]Di Paola, R. A. and Heller, A., Dominical categories: recursion theory without elements, this Journal, vol. 52 (1987), pp. 594–635.Google Scholar
[HIN]Hinman, P. G., Recursion-theoretic hierarchies, Perspectives in Mathematical Logic, Omega Series, Springer-Verlag, Berlin, 1978.CrossRefGoogle Scholar
[MCL]Lane, S. Mac, Categories for the working mathematician, Springer-Verlag, Berlin, 1971.CrossRefGoogle Scholar
[MYH]Myhill, J., Creative sets, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 1 (1955), pp. 97–108.CrossRefGoogle Scholar
[ROG]Rogers, H. Jr., Theory of recursive functions and effective computability, Mc Graw-Hill, New York, 1967.Google Scholar
[WAD]Wadge, W. W., Reducibility and determinateness on the Baire space, Ph.D. thesis, University of California, Berkeley, California, 1984.Google Scholar