Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T19:06:33.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Creatures on ω1 and weak diamonds

Published online by Cambridge University Press:  12 March 2014

Heike Mildenberger
Heike Mildenberger*
Affiliation:
Universität Wien, Kurt Gödel Research Center for Mathematical Logic, Währinger Str. 25, A-1090 Vienna, Austria, E-mail: heike@logic.univie.ac.at
Get access Rights & Permissions [Opens in a new window]

Abstract

We specialise Aronszajn trees by an ωω-bounding forcing that adds reals. We work with creature forcings on uncountable spaces.

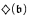As an application of these notions of forcing, we answer a question of Moore, Hrušák and Džamonja whether implies the existence of a Souslin tree in a negative way by showing that “ 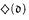and every Aronszajn tree is special” is consistent relative to ZFC.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 74 , Issue 1 , March 2009 , pp. 1 - 16
Copyright
Copyright © Association for Symbolic Logic 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baumgartner, James, Iterated forcing, Surveys in set theory (Mathias, Adrian, editor), London Mathematical Society Lecture Notes Series, vol. 8, Cambridge University Press, 1983, pp. 1–59.Google Scholar
[2]Baumgartner, James and Laver, Richard, Iterated perfect-set forcing, Annals of Mathematical Logic, vol. 17 (1979), pp. 271–288.CrossRefGoogle Scholar
[3]Blass, Andreas and Shelah, Saharon, There may be simple - and -points and the Rudin-Keisler ordering may be downward directed, Annals of Pure and Applied Logic, vol. 33 (1987), pp. 213–243, [BsSh:242].CrossRefGoogle Scholar
[4]Hirschorn, James, Random trees under CH, Israel Journal of Mathematics, vol. 157 (2007), pp. 123–154.CrossRefGoogle Scholar
[5]Hrušák, Michael, Life in the Sacks model, Acta Univ. Carotin. Math. Phys., vol. 42 (2001), pp. 43–58.Google Scholar
[6]Jech, Thomas, Set theory, Addison Wesley, 1978.Google Scholar
[7]Jensen, Ronald B., The fine structure of the constructible hiercharchy, Annals of Mathematical Logic, vol. 4 (1972), pp. 229–308.CrossRefGoogle Scholar
[8]Laver, Richard, Random reals and Souslin trees, Proceedings of the American Mathematical Society, vol. 100 (1987), no. 3, pp. 531–534.CrossRefGoogle Scholar
[9]Mildenberger, Heike and Shelah, Saharon, Specializing Aronszajn trees by countable approximations, Archive for Mathematical Logic, vol. 42 (2003), pp. 627–648.CrossRefGoogle Scholar
[10]Moore, Justin Tatch, Hrušák, Michael, and Džamonja, Mirna, Parametrized ⟡ principles, Transactions of the American Mathematical Society, vol. 356 (2004), pp. 2281–2306.CrossRefGoogle Scholar
[11]Rosłanowski, Andrzej and Shelah, Saharon, Norms on possibilities II, more ccc ideals on 2ω, Journal of Applied Analysis, vol. 3 (1997), pp. 103–127.CrossRefGoogle Scholar
[12]Rosłanowski, Andrzej and Shelah, Saharon, Norms on possibilities I: Forcing with trees and creatures, vol. 141, Memoirs of the American Mathematical Society, no. 671, AMS, 1999.Google Scholar
[13]Rosłanowski, Andrzej and Shelah, Saharon, Measured creatures, Israel Journal of Mathematics, vol. 151 (2006), pp. 61–110.CrossRefGoogle Scholar
[14]Rosłanowski, Andrzej and Shelah, Saharon, Sheva-sheva-sheva: large creatures, Israel Journal of Mathematics, vol. 159 (2007), pp. 109–174.CrossRefGoogle Scholar
[15]Shelah, Saharon, Proper and improper forcing, 2nd ed., Springer, 1998.CrossRefGoogle Scholar