Cylindric algebras with terms

Extract

In this paper we discuss cylindric algebras with terms. The setting is two—sorted algebras—one sort for terms and one for Boolean elements. As with cylindric algebras, a cylindric algebra with terms has its roots in first order predicate logic [HMT1].

Let Σ be a set of sentences in a first order language with terms, equality and variables u₀,u₁,u₂, …, Define a relation ≡_Σ on Fm, the set of formulas, by φ ≡_Σθ if and only if Σ ⊢ φ ↔ θ, and on Tm, the set of terms, by τ ≡_Σσ if and only if Σ ⊢ τ ≈ σ. The operations +, ·, c_κ, 0, 1 are defined as usual on equivalence classes. Define 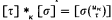, where 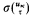is σ with τ substituted for all occurrences of u_κ. That the operation *_κ, for κ < α, is well defined follows from the first order axioms of equality. Let v_κ = [u_κ]. To establish the link between terms and Booleans, define operations o_κ as follows: 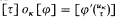, where φ' is a variant of φ such that u_κ is free for τ in φ′ and 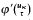is φ′ with τ substituted for all free occurrences of u_κ in φ′. From the first order axioms it follows that o_κ, for κ < α, is well defined. Finally, instead of diagonal elements, we define a Boolean-valued operation on terms as follows: [τ] e [σ] = [τ ≈ σ].