Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T18:54:10.892Z Has data issue: false hasContentIssue false
  • English
  • Français

The decision problem for formulas in prenex conjunctive normal form with binary disjunctions

Published online by Cambridge University Press:  12 March 2014

M. R. Krom
M. R. Krom*
Affiliation:
University of California, Davis
Get access Rights & Permissions [Opens in a new window]

Extract

In [8] S. J. Maslov gives a positive solution to the decision problem for satisfiability of formulas of the form

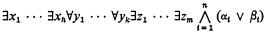
in any first-order predicate calculus without identity where h, k, m, n are positive integers, αi, βi are signed atomic formulas (atomic formulas or negations of atomic formulas), and ∧, ∨ are conjunction and disjunction symbols, respectively (cf. [6] for a related solvable class). In this paper we show that the decision problem is unsolvable for formulas that are like those considered by Maslov except that they have prefixes of the form ∀x∃y1 … ∃yk∀z. This settles the decision problems for all prefix classes of formulas for formulas that are in prenex conjunctive normal form in which all disjunctions are binary (have just two terms). In our concluding section we report results on decision problems for related classes of formulas including classes of formulas in languages with identity and we describe some special properties of formulas in which all disjunctions are binary including a property that implies that any proof of our result, that a class of formulas is a reduction class for satisfiability, is necessarily indirect. Our proof is based on an unsolvable combinatorial tag problem.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 35 , Issue 2 , June 1970 , pp. 210 - 216
Copyright
Copyright © Association for Symbolic Logic 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Chang, C. C. and Keisler, H. J., An improved prenex normal form, this Journal, vol. 27 (1962), pp. 317–326.Google Scholar
[2]Cocke, John and Minsky, Marvin, Universality of tag systems with P = 2, Journal of the Association for Computing Machinery, vol. 11 (1964), pp. 15–20.CrossRefGoogle Scholar
[3]Herbrand, J., Sur le problème fondamental de la logique mathématique, Comptes Rendus des Séances de la Société des Sciences et des Lettres de Varsovie Classe III, vol. 24 (1931), pp. 12–56.Google Scholar
[4]Krom, M. R., A property of sentences that define quasi-order, Notre Dame journal of formal logic, vol. 7 (1966), pp. 349–352.CrossRefGoogle Scholar
[5]Krom, M. R., Some interpolation theorems for first-order formulas in which all disjunctions are binary, Logique et analyse, vol. 43 (1968), pp. 403–412.Google Scholar
[6]Krom, M. R., The decision problem for a class of first-order formulas in which all disjunctions are binary, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 13 (1967), pp. 15–20.CrossRefGoogle Scholar
[7]Krom, M. R., The decision problem for segregated formulas in first-order logic, Mathematica scandinavica, vol. 21 (1967), pp. 233–240.CrossRefGoogle Scholar
[8]Maslov, S. Ju., An inverse method of establishing deducibilities in the classical predicate calculus, Doklady Akademii Nauk SSSR, vol. 159 (1964), pp. 1420–1424.Google Scholar
[9]Robinson, Abraham, Introduction to model theory and to the metamathematics of algebra, North-Holland, Amsterdam, 1963.Google Scholar
[10]Wang, Hao, On denumerable bases of formal systems, Mathematical interpretation of formal systems, North-Holland, Amsterdam, 1955, pp. 57–84.CrossRefGoogle Scholar
[11]Wang, Hao, Tag systems and lag systems, Mathematische Annalen, vol. 152 (1963), pp. 65–74.CrossRefGoogle Scholar