Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T08:10:53.328Z Has data issue: false hasContentIssue false
  • English
  • Français

Definability in well quasi-ordered sets of structures

Published online by Cambridge University Press:  12 March 2014

Charles K. Landraitis
Charles K. Landraitis*
Affiliation:
Boston College, Boston, Massachusetts 02167
Get access Rights & Permissions [Opens in a new window]

Extract

The theorem introduced here provides a sufficient condition for an axiomatic class to be elementary. It resulted from consideration of a definability problem in 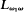, but is introduced in a less specific context and accompanied by applications to .

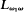As in [La, 1], [La, 2], a reflexive, transitive binary relation R on a nonempty set S will be called a quasi-ordering or q.o. of S. A set of pairwise incomparable elements of S is an antichain and a subset of S linearly ordered by R is a chain. A chain {Si: i ∈ ω} with i > j if and only if (siRsj ∧ ¬ sjRSi) will be called an infinite descending chain. If S has no infinite antichains nor any infinite descending chains, S is well quasi-ordered by R, and is called a well quasi-ordering or w.q.o. Any subset of a w.q.o. is a w.q.o. An element s of a q.o. S is minimal in S if ∀t ∈ S(tRs → sRt). A subset S′ of S is a foundation for S if ∀t ∈ S∃s ∈ S′(sRt).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 42 , Issue 2 , June 1977 , pp. 289 - 291
Copyright
Copyright © Association for Symbolic Logic 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ba]Barwise, J., Remarks on universal sentences of , Duke Mathematics Journal, vol. 36 (1969), pp. 631–637.Google Scholar
[Ke]Keisler, H. J., Model theory for infinitary logic, North-Holland, Amsterdam, 1971.Google Scholar
[La, 1]Laver, R., On Fraisse's order type conjecture, Annals of Mathematics, vol. 93 (1971), pp. 89–111.CrossRefGoogle Scholar
[La, 2]Laver, R., Better quasi-ordering and a class of trees (to appear).Google Scholar
[Mo]Morely, M., Applications of topology to , Proceedings of the Tarski Symposium, Proceedings of Symposia in Pure Mathematics, vol. 25, University of California, Berkeley, 1971, pp. 233–240, American Mathematical Society, Providence, Rhode Island, 1974.Google Scholar