Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-13T08:11:11.402Z Has data issue: false hasContentIssue false
  • English
  • Français

Definability of models by means of existential formulas without identity

Published online by Cambridge University Press:  12 March 2014

Paweł Pazdyka
Paweł Pazdyka*
Affiliation:
Institute of Mathematics, Nicholas Copernicus University, 87-100 Toruń, Poland
Get access Rights & Permissions [Opens in a new window]

Extract

The problem of coding relations by means of a single binary relation is well known in the mathematical literature. It was considered in interpretation theory, and also in connection with investigations of decidability of elementary theories. Using various constructions (see, e.g., [2,6], proofs of Theorem 11 in [7] and Theorem 16.51 in [3]), for any model 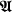for a countable language, one can construct a model 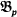for ℒp (a language with a single binary relation symbol 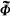) in which 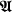is interpretable. Each of the mentioned constructions has the same weak point: the universe of 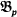is different than the universe of 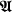. In [4] we have shown that, in the infinite case, one can eliminate this defect, i.e., for any infinite 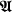, we have constructed a model 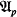, having the same universe as 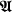, in which 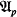is elementarily definable. 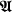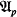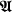In all constructions mentioned above, it appears that formulas, which define in ( in 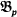), are very complicated. In the present paper, another construction of a model for ℒp is given.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 2 , June 1993 , pp. 424 - 434
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chang, C. C. and Keisler, H. J., Model Theory, North-Holland, Amsterdam, 1973.Google Scholar
[2]Hauschild, K. and Rautenberg, W., Interpretierbarkeit in der Gruppentheorie, Algebra Universalis, vol. 1 (1971), pp. 136–151.CrossRefGoogle Scholar
[3]Monk, D., Mathematical Logic, Springer-Verlag, New York, Heidelberg, Berlin, 1976.CrossRefGoogle Scholar
[4]Pazdyka, P., On a reconstruction of models in models with only one binary relation, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 34 (1988), pp. 449–462.CrossRefGoogle Scholar
[5]Pazdyka, P., On a reconstruction of models in models with only one binary relation: A correction. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 35 (1989), p. 573.CrossRefGoogle Scholar
[6]Rautenberg, W. and Hauschild, K., Interpretierbarkeit und Entscheidbarkeit in der Graphen-theorie I, vol. 17 (1971), pp. 47–55.Google Scholar
[7]Szczerba, L. W., Interpretability of elementary theories, Logic. Foundations of mathematics and computability theory, Reidel, Dordrecht, 1977, pp. 129–145.CrossRefGoogle Scholar