Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T19:12:34.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Definability problems for modules and rings1

Published online by Cambridge University Press:  12 March 2014

Gabriel Sabbagh  and
Paul Eklof
Gabriel Sabbagh
Affiliation:
University of Wisconsin, Madison, Wisconsin 53706
Paul Eklof
Affiliation:
University of Wisconsin, Madison, Wisconsin 53706
Get access Rights & Permissions [Opens in a new window]

Extract

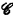This paper is concerned with questions of the following kind: let L be a language of the form Lαω and let be a class of modules over a fixed ring or a class of rings; is it possible to define 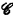in L? We will be mainly interested in the cases where L is Lωω or L∞ω and 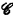is a familiar class in homologic algebra or ring theory.

In Part I we characterize the rings Λ such that the class of free (respectively projective, respectively flat) left Λ-modules is elementary. In [12] we solved the corresponding problems for injective modules; here we show that the class of injective Λ-modules is definable in L∞ω if and only if it is elementary. Moreover we identify the right noetherian rings Λ such that the class of projective (respectively free) left Λ-modules is definable in L∞ω.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 36 , Issue 4 , December 1971 , pp. 623 - 649
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

During the writing of this paper at Yale University the second author was supported by a grant of the Lebanese Council for Scientific Research.

References

[1]Azumaya, G., Corrections and supplementaries to my paper concerning Krull-Remak-Schmidt's theorem, Nagoya Mathematical Journal, vol. 1 (1950), pp. 117–124.CrossRefGoogle Scholar
[2]Barwise, J. and Eklof, P., Infinitary properties of abelian torsion groups. Annals of Mathematical Logic vol. 2 (1970), pp. 25–68.CrossRefGoogle Scholar
[3]Bass, H., Finitistic dimension and a homological generalization of semiprimary rings, Transactions of the American Mathematical Society, vol. 95 (1960), pp. 466–488.CrossRefGoogle Scholar
[4]Björk, J. E., Rings satisfying a minimum condition on principal ideals, Journal für die reine und angewandte Mathematik, vol. 236 (1969), pp. 112–119.Google Scholar
[4]Bourbaki, N., Algèbre, Chap. 2, Algèbre linéaire, troisième edition, Hermann, Paris, 1962.Google Scholar
[5]Bourbaki, N., Algèbre, Chap. 8, Modules et anneaux semi-simples, Hermann, Paris, 1958.Google Scholar
[6]Bourbaki, N., Algèbre commutative, Chaps. 1 and 2, Hermann, Paris, 1961.Google Scholar
[7]Cartan, H. and Eilenberg, S., Homological algebra, Princeton University Press, Princeton, N.J., 1956.Google Scholar
[8]Chase, S. U., Direct products of modules, Transactions of the American Mathematical Society, vol. 97 (1960), pp. 457–473.CrossRefGoogle Scholar
[9]Cohn, P. M., On the free product of associative rings, Mathematische Zeitschrift, vol. 71 (1959), pp. 380–398.CrossRefGoogle Scholar
[10]Cohn, P. M., Some remarks on the invariant basis property, Topology, vol. 5 (1966), pp. 215–228.CrossRefGoogle Scholar
[11]Eilenberg, S., Homological dimension and syzygies, Annals of Mathematics, vol. 64 (1956), pp. 328–336.CrossRefGoogle Scholar
[12]Eklof, P. and Sabbagh, G., Model-completions and modules, Annals of Mathematical Logic, vol. 2 (1971), pp. 251–295.CrossRefGoogle Scholar
[13]Feferman, S. and Vaught, R. L., The first order properties of products of algebraic systems, Fundamenta Mathematicae, vol. 47 (1959), pp. 57–103.CrossRefGoogle Scholar
[14]Fuchs, L., Abelian groups, Pergamon Press, Oxford, 1960.Google Scholar
[15]Govorov, V. E., Rings over which flat modules are free (Russian), Doklady Akademii Nauk SSSR, vol. 144 (1962), pp. 965–967.Google Scholar
[16]Jategaonkar, A. V., A counter-example in ring theory and homological algebra, Journal of Algebra, vol. 12 (1969), pp. 418–440.CrossRefGoogle Scholar
[17]Kaplansky, I., Projective modules, Annals of Mathematics, vol. 68 (1958), pp. 372–377.CrossRefGoogle Scholar
[18]Karp, C. R., Languages with expressions of infinite length, North-Holland, Amsterdam, 1964.Google Scholar
[19]Karp, C. R., Finite-quantifier equivalence, The theory of models, North-Holland, Amsterdam, 1965.Google Scholar
[20]Lenzing, H., Direkte Produkte von freien Moduln, Mathematische Zeitschrift, vol. 106 (1968), pp. 206–212.CrossRefGoogle Scholar
[21]Lenzing, H., Über kohärente Ringe, Mathematische Zeitschrift, vol. 114 (1970), pp. 201–212.CrossRefGoogle Scholar
[22]Lopez-Escobar, E. G. K., An addition to: “On defining well-orderings”, Fundamenta Mathematicae, vol. 59 (1966), pp. 299–300.CrossRefGoogle Scholar
[23]Matlis, E., Injective modules over Noetherian rings, Pacific Journal of Mathematics, vol. 8 (1958), pp. 511–528.CrossRefGoogle Scholar
[24]Morita, K., Kawada, Y. and Tachikawa, H., On injective modules, Mathematische Zeitschrift, vol. 68 (1957), pp. 217–226.CrossRefGoogle Scholar
[25]Osofsky, B. L., A generalization of quasi-Frobenius rings, Journal of Algebra, vol. 4 (1966), pp. 373–387.CrossRefGoogle Scholar
[26]Szmtelew, W., Elementary properties of Abelian groups, Fundamenta Mathematicae, vol. 41 (1955), pp. 203–271.CrossRefGoogle Scholar
[27]Zariski, O. and Samuel, P., Commutative Algebra, vol. I, Van Nostrand, Princeton, N.J., 1958.Google Scholar