Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T02:46:05.567Z Has data issue: false hasContentIssue false
  • English
  • Français

DEFINABLE HENSELIAN VALUATION RINGS

Published online by Cambridge University Press:  22 December 2015

ALEXANDER PRESTEL
ALEXANDER PRESTEL*
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF KONSTANZ KONSTANZ, GERMANYE-mail: alex.prestel@uni-konstanz.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We give model theoretic criteria for the existence of ∃∀ and ∀∃- formulas in the ring language to define uniformly the valuation rings ${\cal O}$ of models 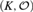$\left( {K,\,{\cal O}} \right)$ of an elementary theory Σ of henselian valued fields. As one of the applications we obtain the existence of an ∃∀-formula defining uniformly the valuation rings ${\cal O}$ of valued henselian fields 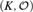$\left( {K,\,{\cal O}} \right)$ whose residue class field k is finite, pseudofinite, or hilbertian. We also obtain ∀∃-formulas φ2 and φ4 such that φ2 defines uniformly k[[t]] in k(t) whenever k is finite or the function field of a real or complex curve, and φ4 replaces φ2 if k is any number field.

Keywords

definabilityvaluation rings
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 4 , December 2015 , pp. 1260 - 1267
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anscombe, W. and Koenigsmann, J., An existential Ø-definition of ${F_q}\left[ {\left[ t \right]} \right]$in ${F_q}\left( {\left( t \right)} \right)$, this Journal, 2014.Google Scholar
Ax, J., On the undecidability of power series fields. Proceedings of the American Mathematical Society, vol. 16 (1965), p. 846.Google Scholar
Ax, J., The elementary theory of finite fields, Annals of Mathematics, vol. 88 (1968), pp. 239–271.CrossRefGoogle Scholar
Cluckers, R., Deraskhshan, J., Leenknegt, E., and Macintyre, A., Uniformly defining valuation rings in henselian valued fields with finite or pseudo-finite residue fields. Annals of Pure and Applied Logic, vol. 164 (2013), pp. 1236–1246.CrossRefGoogle Scholar
Elman, R., Karpenko, N., and Merkurjev, A., The algebraic and geometric theory of quadratic forms, vol. 56, AMS, College Publications, AMS Colloquium Publications, Providence, PA, 2008.Google Scholar
Engler, A. and Prestel, A., Valued Fields, Springer, Berlin-Heidelberg, 2005.Google Scholar
Ershov, Y.L., Relative regular closedness and π-valuations. Algebra and Logic, vol. 31 (1992), vol. 6, pp. 140–146.Google Scholar
Fehm, A., Existential Ø-definability of henselian valuation rings, this Journal, ArXiv 1307.1956v2, 2014, to appear.Google Scholar
Fried, M.D. and Jarden, M., Field arithmetic, second edition, Springer, Berlin-Heidelberg, 2001.Google Scholar
Hong, J., Definable non-divisible Henselian valuations. Bulletin of the London Mathematical Society, vol. 46 (2014), no 1, p. 1418.CrossRefGoogle Scholar
Prestel, A. and Delzell, C.N., Positive polynomials, Springer, Berlin-Heidelberg, 2001.CrossRefGoogle Scholar
Roquette, P., Nonstandard aspects of Hilbert’s Irreducibility Theorem, Lecture Notes in Mathematics, vol. 498, pp. 231–275, Springer, Berlin-Heidelberg-New York, 1975.Google Scholar