Article contents
DEGREES OF CATEGORICITY ON A CONE VIA η-SYSTEMS
Published online by Cambridge University Press: 21 March 2017
Abstract
We investigate the complexity of isomorphisms of computable structures on cones in the Turing degrees. We show that, on a cone, every structure has a strong degree of categoricity, and that degree of categoricity is 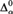 ${\rm{\Delta }}_\alpha ^0 $ -complete for some α. To prove this, we extend Montalbán’s η-system framework to deal with limit ordinals in a more general way. We also show that, for any fixed computable structure, there is an ordinal α and a cone in the Turing degrees such that the exact complexity of computing an isomorphism between the given structure and another copy
${\rm{\Delta }}_\alpha ^0 $ -complete for some α. To prove this, we extend Montalbán’s η-system framework to deal with limit ordinals in a more general way. We also show that, for any fixed computable structure, there is an ordinal α and a cone in the Turing degrees such that the exact complexity of computing an isomorphism between the given structure and another copy  ${\cal B}$ in the cone is a c.e. degree in
${\cal B}$ in the cone is a c.e. degree in 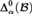 ${\rm{\Delta }}_\alpha ^0\left( {\cal B} \right)$ . In each of our theorems the cone in question is clearly described in the beginning of the proof, so it is easy to see how the theorems can be viewed as general theorems with certain effectiveness conditions.
${\rm{\Delta }}_\alpha ^0\left( {\cal B} \right)$ . In each of our theorems the cone in question is clearly described in the beginning of the proof, so it is easy to see how the theorems can be viewed as general theorems with certain effectiveness conditions.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
- 8
- Cited by

