Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T06:44:44.616Z Has data issue: false hasContentIssue false
  • English
  • Français

Degrees of monotone complexity

Published online by Cambridge University Press:  12 March 2014

William C. Calhoun
William C. Calhoun*
Affiliation:
Department of Mathematics, Computer Science and Statistics, Bloomsburg University, Bloomsburg, PA 17815., USA, E-mail: wcalhoun@bloomu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Levin and Schnorr (independently) introduced the monotone complexity, Km (α), of a binary string α. We use monotone complexity to define the relative complexity (or relative randomness) of reals. We define a partial ordering ≤Km on 2ω by α ≤Km β iff there is a constant c such that Km(α | n) ≤ Km(β | n)+ c for all n. The monotone degree of α is the set of all β such that α Km β and β Km α. We show the monotone degrees contain an antichain of size 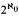, a countable dense linear ordering (of degrees of cardinality 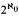), and a minimal pair.

Downey, Hirschfeldt, LaForte, Nies and others have studied a similar structure, the K-degrees, where K is the prefix-free Kolmogorov complexity. A minimal pair of K-degrees was constructed by Csima and Montalban. Of particular interest are the noncomputable trivial reals, first constructed by Solovay. We defineareal to be (Km,K)-trivial if for some constant c, Km(α | n) ≤ K(n) + c for all n. It is not known whether there is a Km-minimal real, but we show that any such real must be (Km,K)-trivial.

Finally, we consider the monotone degrees of the computably enumerable (c.e.) and strongly computably enumerable (s.c.e.) reals. We show there is no minimal c.e. monotone degree and that Solovay reducibility does not imply monotone reducibility on the c.e. reals. We also show the s.c.e. monotone degrees contain an infinite antichain and a countable dense linear ordering.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 71 , Issue 4 , December 2006 , pp. 1327 - 1341
Copyright
Copyright © Association for Symbolic Logic 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Becher, V., Figueira, S., Nies, A., and Picchi, S., Program size complexity for possibly infinite computations, Notre Dame Journal of Formal Logic, vol. 46 (2005), pp. 51–64.CrossRefGoogle Scholar
[2]Chaitin, G. J., On the length of programs for computing finite binary sequences, Journal of the ACM, vol. 13 (1966), pp. 547–569.CrossRefGoogle Scholar
[3]Chaitin, G. J., On the length of programs for computing finite binary sequences: statistical considerations, Journal of the ACM, vol. 16 (1969), pp. 145–159.CrossRefGoogle Scholar
[4]Chaitin, G. J., A theory of program size formally identical to information theory, Journal of the ACM, vol. 22 (1975), pp. 329–340.CrossRefGoogle Scholar
[5]Csima, B. F. and Montalbán, A., A minimal pair of K-degrees, Proceedings of the American Mathematical Society, vol. 134 (2006), pp. 1499–1502.CrossRefGoogle Scholar
[6]Downey, R. G. and Hirschfeldt, D. R., Algorithmic randomness and complexity, Springer-Verlag, to appear.Google Scholar
[7]Downey, R. G., Hirschfeldt, D. R., and LaForte, G., Randomness and reducibility, Mathematical Foundations of Computer Science 2001 (Sgall, J., Pultr, A., and Kolman, P., editors), Lecture Notes in Computer Science, vol. 2136, Springer-Verlag, 2003, pp. 316–327.CrossRefGoogle Scholar
[8]Downey, R. G., Hirschfeldt, D. R., and Nies, A., Randomness, computability and density, SIAM Journal on Computing, vol. 31 (2002), pp. 1169–1183.CrossRefGoogle Scholar
[9]Downey, R. G, Hirschfeldt, D. R., Nies, A., and Stephan, F., Trivial reals. Proceedings of Asian Logic Conferences (Downey, R. G.et al., editors), World Scientific, 2003, pp. 103–131.CrossRefGoogle Scholar
[10]Gács, P., On the symmetry of algorithmic information, Soviet Mathematics Doklady, vol. 15 (1974), pp. 1477–1480.Google Scholar
[11]Kolmogorov, A. N., Three approaches to the quantitative definition of information, Problems of Information Transmission, vol. 1 (1965), pp. 1–7.Google Scholar
[12]Kummer, M., Kolmogorov complexity and instance complexity of recursively enumerable sets, SIAM Journal on Computing, vol. 25 (1996), pp. 1123–1143.CrossRefGoogle Scholar
[13]Levin, L. A., On the notion of a random sequence, Soviet Mathematics Doklady, vol. 14 (1973), pp. 1413–1416.Google Scholar
[14]Levin, L. A., Laws of information conservation (non-growth) and aspects of the foundation of probability theory, Problems of Information Transmission, vol. 10 (1974), pp. 206–210.Google Scholar
[15]Li, M. and Vitányi, P., An introduction to Kolmogorov complexity and its applications, 2nd ed., Springer-Verlag, 1997.CrossRefGoogle Scholar
[16]Loveland, D. W., A variant of the Kolmogorov concept of complexity, Information and Control, vol. 15 (1969), pp. 510–526.CrossRefGoogle Scholar
[17]Miller, J. S., Every 2-random real is Kolmogorov random, this Journal, vol. 69 (2004), pp. 907–913.Google Scholar
[18]Miller, J. S. and Yu, L., On initial segment complexity and degrees of randomness, Transaction of the American Mathematical Society, to appear.Google Scholar
[19]Nies, A., Lowness properties and randomness, Advances in Mathematics, vol. 197 (2005), pp. 274–305.CrossRefGoogle Scholar
[20]Nies, A., Stephan, F., and Terwijn, S., Randomness, relativization and turing degrees, this Journal, vol. 70 (2005), pp. 515–535.Google Scholar
[21]Sacks, G. E., The recursively enumerable degrees are dense, Annals of Mathematics, vol. 80 (1964), pp. 300–312.CrossRefGoogle Scholar
[22]Schnorr, C. P., Process complexity and effective random tests, Journal of Computer and System Sciences, vol. 7 (1973), pp. 376–388.CrossRefGoogle Scholar
[23]Schnorr, C. P., A survey of the theory of random sequences, Basic problems in methodology and linguistics (Butts, R. E. and Hintikka, J., editors), D. Reidel, 1977, pp. 193–210.CrossRefGoogle Scholar
[24]Solomonoff, R. J., A formal theory of inductive inference, part 1 and part 2, Information and Control, vol. 7 (1964), pp. 1–22 and 224–254.CrossRefGoogle Scholar
[25]Solovay, R. M., Draft of a paper (or series of papers) on Chaitin's work, Unpublished manuscript, 1975, IBM Thomas J. Watson Research Center, NY.Google Scholar
[26]Uspensky, V. A. and Shen, A., Relations between varieties of Kolmogorov complexities, Mathematical Systems Theory, vol. 29 (1996), pp. 271–292.CrossRefGoogle Scholar