Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T19:34:00.568Z Has data issue: false hasContentIssue false
  • English
  • Français

Degrees of sensible lambda theories

Published online by Cambridge University Press:  12 March 2014

Henk Barendregt ,
Jan Bergstra ,
Jan Willem Klop  and
Henri Volken
Henk Barendregt
Affiliation:
Mathematics Institute, Utrecht, Netherlands
Jan Bergstra
Affiliation:
Mathematics Institute, Utrecht, Netherlands
Jan Willem Klop
Affiliation:
Mathematics Institute, Utrecht, Netherlands
Henri Volken
Affiliation:
Mathematics Institute, Utrecht, Netherlands
Get access Rights & Permissions [Opens in a new window]

Summary

A λ-theory T is a consistent set of equations between λ-terms closed under derivability. The degree of T is the degree of the set of Gödel numbers of its elements. 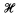is the λ-theory axiomatized by the set {M = N∣ M, N unsolvable}. A λ-theory is sensible iff T ⊃ 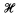; for a motivation see [6] and [4].

In §1 it is proved that the theory 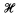is Σ20-complete. We present Wadsworth's proof that its unique maximal consistent extension 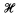* (= Th(D∞)) is Π20-complete. In §2 it is proved that 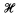η (= λη-calculus + 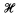) is not closed under the ω-rule (see [1]). In §3 arguments are given to conjecture that 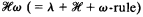is Π11-complete. This is done by representing recursive sets of sequence numbers as λ-terms and by connecting wellfoundedness of trees with provability in 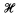ω. In §4 an infinite set of equations independent over 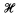η will be constructed. From this it follows that there are 2ℵ0 sensible theories T such that 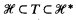and 2ℵ0 sensible hard models of arbitrarily high degrees. In §5 some nonprovability results needed in §§1 and 2 are established. For this purpose one uses the theory 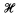η extended with a reduction relation for which the Church–Rosser theorem holds. The concept of Gross reduction is used in order to show that certain terms have no common reduct.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 1 , March 1978 , pp. 45 - 55
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barendregt, H. P., Combinatory logic and the ω-rule, Fundamenta Mathematicae, vol. 82 (1974), pp. 199–215.CrossRefGoogle Scholar
[2]Barendregt, H. P., The type free lambda calculus, Handbook of mathematical logic, North-Holland, Amsterdam, 1977 (to appear).Google Scholar
[3]Barendregt, H. P., Bergstra, J. A., Klop, J. W. and Volken, H., Some notes on lambda-reduction, preprint 22, Department of Mathematics, University of Utrecht.Google Scholar
[4]Barendregt, H. P., Solvability in λ-calculi, Proceedings of the Logic Conference, Clermont-Ferrand, 1975 (Guillaume, M., Editor).Google Scholar
[5]Barendregt, H. P., The lambda calculus, North-Holland, Amsterdam (to appear).Google Scholar
[6]Hyland, J. M. E., A survey of some useful partial order relations on terms of the lambda calculus, λ-calculus ana computer science theory, Springer Lecture Notes in Computer Science, No. 37 (1975), pp. 83–93.CrossRefGoogle Scholar
[7]Plotkin, G., The λ-calculus is ω-incomplete, this Journal, vol. 39 (1974), pp. 313–317.Google Scholar
[8]Rogers, H., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[9]Scott, D., Continuous lattices, Springer Lecture Notes in Mathematics, No. 274, pp. 97–136.Google Scholar
[10]Staples, J., Church-Rosser theorems for replacement systems, Algebra and logic, Springer Lecture Notes in Mathematics, No. 450 (1975), pp. 291–307.Google Scholar
[11]Wadsworth, C., Degrees associated with λ-calculus concepts, handwritten note, 1973.Google Scholar
[12]Wadsworth, C., The relation between lambda-expressions and their denotations, Siam Journal of Computing, vol. 5 (1976), pp. 488–521.CrossRefGoogle Scholar