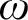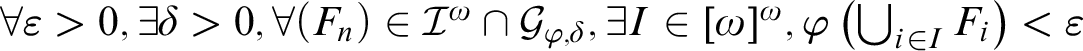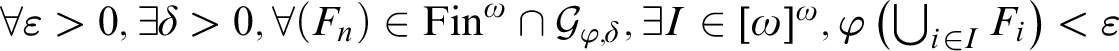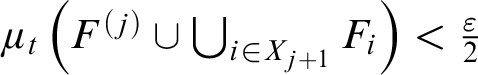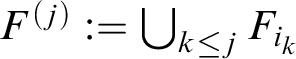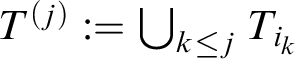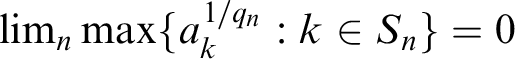1 Introduction
An ideal
![]() $\mathcal {I}$
on the nonnegative integers
$\mathcal {I}$
on the nonnegative integers
![]() $\omega $
is a family of subsets of
$\omega $
is a family of subsets of
![]() $\omega $
closed under finite unions and subsets. Unless otherwise stated, we assume that
$\omega $
closed under finite unions and subsets. Unless otherwise stated, we assume that
![]() $\mathcal {I}$
is admissible (i.e., it contains
$\mathcal {I}$
is admissible (i.e., it contains
![]() $\mathrm {Fin}:=[\omega ]^{<\omega }$
) and proper (i.e.,
$\mathrm {Fin}:=[\omega ]^{<\omega }$
) and proper (i.e.,
![]() $\omega \notin \mathcal {I}$
). An ideal
$\omega \notin \mathcal {I}$
). An ideal
![]() $\mathcal {I}$
is tall if each infinite set
$\mathcal {I}$
is tall if each infinite set
![]() $A\subseteq \omega $
contains an infinite subset in
$A\subseteq \omega $
contains an infinite subset in
![]() $\mathcal {I}$
. It is a P-ideal if it is
$\mathcal {I}$
. It is a P-ideal if it is
![]() $\sigma $
-directed modulo finite sets, i.e., for each sequence
$\sigma $
-directed modulo finite sets, i.e., for each sequence
![]() $(A_n)$
in
$(A_n)$
in
![]() $\mathcal {I}$
there is
$\mathcal {I}$
there is
![]() $A\in \mathcal {I}$
such that
$A\in \mathcal {I}$
such that
![]() $A_n\setminus A$
is finite for all n. Ideals are regarded as subsets of
$A_n\setminus A$
is finite for all n. Ideals are regarded as subsets of
![]() $\{0,1\}^\omega $
with the Cantor-space topology, hence it is possible to speak about Borel, analytic ideals, etc. We refer to [Reference Hrušák11, Reference Uzcátegui Aylwin27] for recent surveys on ideals and associated filters.
$\{0,1\}^\omega $
with the Cantor-space topology, hence it is possible to speak about Borel, analytic ideals, etc. We refer to [Reference Hrušák11, Reference Uzcátegui Aylwin27] for recent surveys on ideals and associated filters.
A lower semicontinuous submeasure (lscsm)
![]() $\varphi :\mathcal {P}(\omega ) \to [0,\infty ]$
is a subadditive monotone function such that
$\varphi :\mathcal {P}(\omega ) \to [0,\infty ]$
is a subadditive monotone function such that
![]() $\varphi (\emptyset )=0$
,
$\varphi (\emptyset )=0$
,
![]() $\varphi (\{n\})<\infty $
for all
$\varphi (\{n\})<\infty $
for all
![]() $n\in \omega $
, and
$n\in \omega $
, and
![]() $\varphi (A)=\lim _n \varphi (A\cap n)$
for all
$\varphi (A)=\lim _n \varphi (A\cap n)$
for all
![]() $A\subseteq \omega $
(here, as usual, each n is identified with
$A\subseteq \omega $
(here, as usual, each n is identified with
![]() $\{0,1,\ldots ,n-1\}$
). Denote by
$\{0,1,\ldots ,n-1\}$
). Denote by
![]() $\mathrm {supp}(\varphi ):=\{n \in \omega : \varphi (\{n\})\neq 0\}$
its support. A lscsm with finite support will be typically denoted by
$\mathrm {supp}(\varphi ):=\{n \in \omega : \varphi (\{n\})\neq 0\}$
its support. A lscsm with finite support will be typically denoted by
![]() $\mu $
. It is folklore that the pointwise supremum of lscsms is a lscsm. For each lscsm
$\mu $
. It is folklore that the pointwise supremum of lscsms is a lscsm. For each lscsm
![]() $\varphi $
, we associate its exhaustive ideal
$\varphi $
, we associate its exhaustive ideal
where
![]() $\|A\|_\varphi :=\inf _{F \in \mathrm {Fin}} \varphi (A\setminus F)$
. A classical result of Solecki states that a (not necessarily proper) ideal
$\|A\|_\varphi :=\inf _{F \in \mathrm {Fin}} \varphi (A\setminus F)$
. A classical result of Solecki states that a (not necessarily proper) ideal
![]() $\mathcal {I}$
is an analytic P-ideal if and only if
$\mathcal {I}$
is an analytic P-ideal if and only if
![]() $\mathcal {I}=\mathrm {Exh}(\varphi )$
for some lscsm
$\mathcal {I}=\mathrm {Exh}(\varphi )$
for some lscsm
![]() $\varphi $
such that
$\varphi $
such that
![]() $\varphi (\omega )<\infty $
, see e.g., [Reference Farah6, Section 1.2] for a textbook exposition. In particular, each analytic P-ideal is
$\varphi (\omega )<\infty $
, see e.g., [Reference Farah6, Section 1.2] for a textbook exposition. In particular, each analytic P-ideal is
![]() $F_{\sigma \delta }$
. Every lscsm
$F_{\sigma \delta }$
. Every lscsm
![]() $\varphi $
defines a metric
$\varphi $
defines a metric
![]() $d_\varphi $
on
$d_\varphi $
on
![]() $\mathcal {I}=\mathrm {Exh}(\varphi )$
given by
$\mathcal {I}=\mathrm {Exh}(\varphi )$
given by
![]() $d_\varphi (A,B)=\varphi (A\triangle B)$
for all
$d_\varphi (A,B)=\varphi (A\triangle B)$
for all
![]() $A,B \in \mathcal {I}$
. The topology induced on
$A,B \in \mathcal {I}$
. The topology induced on
![]() $\mathcal {I}$
is Polish and does not depend on the choice of
$\mathcal {I}$
is Polish and does not depend on the choice of
![]() $\varphi $
, see [Reference Solecki22].
$\varphi $
, see [Reference Solecki22].
The aim of this work is to study the relationship between two families of analytic P-ideals defined below.
Definition 1.1. An ideal
![]() $\mathcal {I}$
is called a generalized density ideal if there exists a sequence
$\mathcal {I}$
is called a generalized density ideal if there exists a sequence
![]() $\boldsymbol {\mu }=(\mu _n)$
of lscsms with finite pairwise disjoint supports such that
$\boldsymbol {\mu }=(\mu _n)$
of lscsms with finite pairwise disjoint supports such that
![]() $\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
, where
$\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
, where
![]() $\varphi _{\boldsymbol {\mu }}:=\sup _n \mu _n$
.
$\varphi _{\boldsymbol {\mu }}:=\sup _n \mu _n$
.
Note that if
![]() $\boldsymbol {\mu }=(\mu _n)$
is a sequence of lscsms with finite pairwise disjoint supports, then
$\boldsymbol {\mu }=(\mu _n)$
is a sequence of lscsms with finite pairwise disjoint supports, then
 $$ \begin{align*}\mathrm{Exh}\left(\varphi_{\boldsymbol{\mu}}\right)=\mathrm{Exh}\left(\limsup_{n\to \infty}\mu_n\right). \end{align*} $$
$$ \begin{align*}\mathrm{Exh}\left(\varphi_{\boldsymbol{\mu}}\right)=\mathrm{Exh}\left(\limsup_{n\to \infty}\mu_n\right). \end{align*} $$
Generalized density ideals have been introduced by Farah in [Reference Farah7, Section 2.10], see also [Reference Farah9], and have been used in different contexts, see e.g., [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Reference Filipów, Mrożek, Recław and Szuca10, Reference Leonetti16]. We remark that Farah’s original definition assumed that
![]() $\{\mathrm {supp}(\mu _n): n \in \omega \}$
is a partition of
$\{\mathrm {supp}(\mu _n): n \in \omega \}$
is a partition of
![]() $\omega $
into finite intervals; however, we will show in Proposition 2.1 that this is equivalent to Definition 1.1. The family of generalized density ideals is very rich. Indeed, if each
$\omega $
into finite intervals; however, we will show in Proposition 2.1 that this is equivalent to Definition 1.1. The family of generalized density ideals is very rich. Indeed, if each
![]() $\mu _n$
is a measure then
$\mu _n$
is a measure then
![]() $\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
is a density ideal, as defined in [Reference Farah6, Section 1.13], cf. also [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Proposition 6.3]. In particular, it includes
$\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
is a density ideal, as defined in [Reference Farah6, Section 1.13], cf. also [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Proposition 6.3]. In particular, it includes
![]() $\emptyset \times \mathrm {Fin}$
, the ideal of density zero sets
$\emptyset \times \mathrm {Fin}$
, the ideal of density zero sets
 $$ \begin{align*}\mathcal{Z}:=\left\{A\subseteq \omega: \lim_{n\to \infty}\frac{|A\cap n|}{n}=0\right\}, \end{align*} $$
$$ \begin{align*}\mathcal{Z}:=\left\{A\subseteq \omega: \lim_{n\to \infty}\frac{|A\cap n|}{n}=0\right\}, \end{align*} $$
and all the Erdős–Ulam ideals introduced by Just and Krawczyk in [Reference Just and Krawczyk12], that is, ideals of the type
![]() $\mathrm {Exh}(\varphi _{f})$
where
$\mathrm {Exh}(\varphi _{f})$
where
![]() $f: \omega \to (0,\infty )$
is a function such that
$f: \omega \to (0,\infty )$
is a function such that
![]() $\sum _{n}f(n)=\infty $
,
$\sum _{n}f(n)=\infty $
,
 $f(n)=o\left (\sum _{i\le n}f(i)\right )$
as
$f(n)=o\left (\sum _{i\le n}f(i)\right )$
as
![]() $n\to \infty $
, and
$n\to \infty $
, and
![]() $\varphi _f: \mathcal {P}(\omega ) \to (0,\infty )$
is the submeasure defined by
$\varphi _f: \mathcal {P}(\omega ) \to (0,\infty )$
is the submeasure defined by
 $$ \begin{align*} \forall A\subseteq \omega,\quad \varphi_f(A)=\sup_{n \in \omega} \frac{\sum_{i\le n,\, i \in A}f(i)}{\sum_{i\le n}f(i)}, \end{align*} $$
$$ \begin{align*} \forall A\subseteq \omega,\quad \varphi_f(A)=\sup_{n \in \omega} \frac{\sum_{i\le n,\, i \in A}f(i)}{\sum_{i\le n}f(i)}, \end{align*} $$
see [Reference Farah6, pp. 42–43]. In addition, this family contains the ideals associated with suitable modifications of the natural asymptotic density, the so-called simple density ideals, see [Reference Balcerzak, Das, Filipczak and Swaczyna2, Reference Kwela, Popławski, Swaczyna and Tryba15] and Section 3. Lastly, a large class of generalized density ideals has been defined by Louveau and Veličković in [Reference Louveau and Veličković17, Reference Louveau and Veličković18], cf. also [Reference Farah7, Section 2.11].
Definition 1.2. An ideal
![]() $\mathcal {I}$
is said to be density-like if
$\mathcal {I}$
is said to be density-like if
![]() $\mathcal {I}=\mathrm {Exh}(\varphi )$
for a density-like lscsm
$\mathcal {I}=\mathrm {Exh}(\varphi )$
for a density-like lscsm
![]() $\varphi $
, that is, a lscsm such that for all
$\varphi $
, that is, a lscsm such that for all
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $\delta>0$
for which, if
$\delta>0$
for which, if
![]() $(F_n) \in \mathrm {Fin}^\omega $
is a sequence of finite pairwise disjoint sets with
$(F_n) \in \mathrm {Fin}^\omega $
is a sequence of finite pairwise disjoint sets with
![]() $\varphi (F_n)<\delta $
for all n, then
$\varphi (F_n)<\delta $
for all n, then
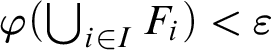 $\varphi (\bigcup _{i \in I}F_i) < \varepsilon $
for some infinite
$\varphi (\bigcup _{i \in I}F_i) < \varepsilon $
for some infinite
![]() $I\subseteq \omega $
.
$I\subseteq \omega $
.
The class of density-like ideals played a role in [Reference Mátrai19, Reference Solecki and Todorcevic25]. The main result of [Reference Solecki and Todorcevic25] states that the ideal
![]() $\mathrm {NWD}$
of all closed nowhere dense subsets of
$\mathrm {NWD}$
of all closed nowhere dense subsets of
![]() $2^\omega $
is not Tukey reducible to any density-like ideal
$2^\omega $
is not Tukey reducible to any density-like ideal
![]() $\mathcal {I}$
(that is, there is no function
$\mathcal {I}$
(that is, there is no function
![]() $f:\mathrm {NWD}\to \mathcal {I}$
such that for each
$f:\mathrm {NWD}\to \mathcal {I}$
such that for each
![]() $A\in \mathcal {I}$
there exists
$A\in \mathcal {I}$
there exists
![]() $B\in \mathrm {NWD}$
for which
$B\in \mathrm {NWD}$
for which
![]() $f(X)\subseteq A$
implies
$f(X)\subseteq A$
implies
![]() $X\subseteq B$
, i.e., preimages of bounded sets are bounded). In particular, this works for
$X\subseteq B$
, i.e., preimages of bounded sets are bounded). In particular, this works for
![]() $\mathcal {Z}$
(since it is a density-like ideal), thus answering old questions of Isbell from 1972 and Fremlin from 1991.
$\mathcal {Z}$
(since it is a density-like ideal), thus answering old questions of Isbell from 1972 and Fremlin from 1991.
It is known that if
![]() $\varphi $
is density-like and
$\varphi $
is density-like and
![]() $\mathrm {Exh}(\varphi )=\mathrm {Exh}(\psi )$
, for some lscsm
$\mathrm {Exh}(\varphi )=\mathrm {Exh}(\psi )$
, for some lscsm
![]() $\psi $
, then
$\psi $
, then
![]() $\psi $
is density-like too. In addition, tall
$\psi $
is density-like too. In addition, tall
![]() $F_\sigma $
P-ideals are not density-like, see [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Fact 5.1], and there exists a nontall
$F_\sigma $
P-ideals are not density-like, see [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Fact 5.1], and there exists a nontall
![]() $F_\sigma $
P-ideal which is not density-like, see [Reference Mátrai19].
$F_\sigma $
P-ideal which is not density-like, see [Reference Mátrai19].
On the one hand, every generalized density ideal
![]() $\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
is a density-like ideal (indeed,
$\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
is a density-like ideal (indeed,
![]() $\varphi _{\boldsymbol {\mu }}$
is a density-like lscsm). On the other hand, the converse has been asked in [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Question 5.11]:
$\varphi _{\boldsymbol {\mu }}$
is a density-like lscsm). On the other hand, the converse has been asked in [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Question 5.11]:
Question 1. Is there a density-like ideal which is not a generalized density ideal?
This question is closely connected to the notion of representability of ideals in Polish Abelian groups and in Banach spaces. Following [Reference Borodulin-Nadzieja, Farkas and Plebanek5], we say that an ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\omega $
is representable in a Polish Abelian group X if there is a function
$\omega $
is representable in a Polish Abelian group X if there is a function
![]() $f:\omega \to X$
such that
$f:\omega \to X$
such that
By [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Theorems 4.1 and 4.4], an ideal is representable in some Polish Abelian group if and only if it is an analytic P-ideal, and it is representable in some Banach space if and only if it is a nonpathological analytic P-ideal (cf. Remark 3.3). Moreover, for instance, it is known that an ideal is representable in
![]() $\mathbb {R}^\omega $
if and only if it is an intersection of countably many summable ideals [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Example 3.8] (i.e., ideals of the form
$\mathbb {R}^\omega $
if and only if it is an intersection of countably many summable ideals [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Example 3.8] (i.e., ideals of the form
 $\mathcal {I}_f:=\left \{A\subseteq \omega :\ \sum _{n\in A}f(n)<\infty \right \}$
for some
$\mathcal {I}_f:=\left \{A\subseteq \omega :\ \sum _{n\in A}f(n)<\infty \right \}$
for some
![]() $f:\omega \to [0,\infty )$
such that
$f:\omega \to [0,\infty )$
such that
![]() $\sum _{n}f(n)=\infty $
); for more on this notion see [Reference Borodulin-Nadzieja, Farkas and Plebanek5]. It is worth mentioning that Borodulin-Nadzieja and Farkas, using representability of ideals in Banach spaces, constructed a new example of a Banach space [Reference Borodulin-Nadzieja and Farkas4, Example 5.9], and strengthened Mazur’s Lemma [Reference Borodulin-Nadzieja and Farkas4, Corollary 7.6], which is a basic tool in Banach space theory (they were able to specify the form of the convex combination in Mazur’s Lemma). This suggests that studying the interplay between representability and theory of analytic P-ideals may have some relevant yet unexploited potential for the study of the geometry of Banach spaces.
$\sum _{n}f(n)=\infty $
); for more on this notion see [Reference Borodulin-Nadzieja, Farkas and Plebanek5]. It is worth mentioning that Borodulin-Nadzieja and Farkas, using representability of ideals in Banach spaces, constructed a new example of a Banach space [Reference Borodulin-Nadzieja and Farkas4, Example 5.9], and strengthened Mazur’s Lemma [Reference Borodulin-Nadzieja and Farkas4, Corollary 7.6], which is a basic tool in Banach space theory (they were able to specify the form of the convex combination in Mazur’s Lemma). This suggests that studying the interplay between representability and theory of analytic P-ideals may have some relevant yet unexploited potential for the study of the geometry of Banach spaces.
Question 1 is motivated by the problem of characterizing ideals which are representable in the Banach space
![]() $c_0$
[Reference Borodulin-Nadzieja, Farkas and Plebanek5, Question 5.10]. It is known that a tall
$c_0$
[Reference Borodulin-Nadzieja, Farkas and Plebanek5, Question 5.10]. It is known that a tall
![]() $F_\sigma $
P-ideal is representable in
$F_\sigma $
P-ideal is representable in
![]() $c_0$
if and only if it is a summable ideal [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Theorem 5.7] and that all nonpathological generalized density ideals are representable in
$c_0$
if and only if it is a summable ideal [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Theorem 5.7] and that all nonpathological generalized density ideals are representable in
![]() $c_0$
[Reference Borodulin-Nadzieja, Farkas and Plebanek5, Example 4.2].
$c_0$
[Reference Borodulin-Nadzieja, Farkas and Plebanek5, Example 4.2].
The motivation of this work is to shed some light on [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Question 5.10] by providing a large class of density-like ideals which are not generalized density ideals. In particular, we give a positive answer to Question 1.
Theorem 1.3. There exists a density-like ideal which is not a generalized density ideal.
More precisely, our main contributions are:
-
(i) There exist uncountably many nonpathological, nontall, and pairwise nonisomorphic density-like ideals which are not generalized density ideals, see Theorem 3.7.
-
(ii) There exist uncountably many nonpathological, tall, and pairwise nonisomorphic density-like ideals which are not generalized density ideals, see Theorem 4.24.
-
(iii) A characterization of generalized density ideals which is reminiscent of the definition of density-like ideals, see Theorem 5.3.
2 Preliminaries
Given (not necessarily proper or admissible) ideals
![]() $\mathcal {I}, \mathcal {J}$
on
$\mathcal {I}, \mathcal {J}$
on
![]() $\omega $
, we let their disjoint sum and Fubini product be
$\omega $
, we let their disjoint sum and Fubini product be
 $$ \begin{align*} \mathcal{I} \oplus \mathcal{J}:=\left\{B\subseteq 2\times\omega: B_{(0)} \in \mathcal{I},B_{(1)} \in \mathcal{J} \right\}, \end{align*} $$
$$ \begin{align*} \mathcal{I} \oplus \mathcal{J}:=\left\{B\subseteq 2\times\omega: B_{(0)} \in \mathcal{I},B_{(1)} \in \mathcal{J} \right\}, \end{align*} $$
 $$ \begin{align*} \mathcal{I} \times \mathcal{J}:=\left\{B\subseteq \omega^2: \{m \in \omega: B_{(m)}\notin \mathcal{J}\} \in \mathcal{I} \right\}, \end{align*} $$
$$ \begin{align*} \mathcal{I} \times \mathcal{J}:=\left\{B\subseteq \omega^2: \{m \in \omega: B_{(m)}\notin \mathcal{J}\} \in \mathcal{I} \right\}, \end{align*} $$
where
![]() $B_{(m)}:=\{k \in \omega : (m,k) \in B\}$
. Then
$B_{(m)}:=\{k \in \omega : (m,k) \in B\}$
. Then
![]() $\mathcal {I}\times \mathcal {J}$
is an ideal on
$\mathcal {I}\times \mathcal {J}$
is an ideal on
![]() $\omega ^2$
. We identify ideals on
$\omega ^2$
. We identify ideals on
![]() $\omega ^2$
with ideals on
$\omega ^2$
with ideals on
![]() $\omega $
through the bijection
$\omega $
through the bijection
![]() $h: \omega ^2 \to \omega $
defined by
$h: \omega ^2 \to \omega $
defined by
To ease the notation, we define the families
![]() $\mathcal {F}_{\mathrm {disj}}$
,
$\mathcal {F}_{\mathrm {disj}}$
,
![]() $\mathcal {F}_{\mathrm {incr}}$
, and
$\mathcal {F}_{\mathrm {incr}}$
, and
![]() $\mathcal {F}_{\mathrm {int}}$
of sequences of nonempty finite sets which are, respectively, pairwise disjoint, increasing, and increasing intervals:
$\mathcal {F}_{\mathrm {int}}$
of sequences of nonempty finite sets which are, respectively, pairwise disjoint, increasing, and increasing intervals:
 $$ \begin{align*} \begin{split} \mathcal{F}_{\mathrm{disj}}:=&\{(F_n) \in (\mathrm{Fin}\setminus \{\emptyset\})^\omega: \forall \{i,j\} \in [\omega]^2, F_i \cap F_j=\emptyset\},\\ \mathcal{F}_{\mathrm{incr}}:=&\{(F_n) \in \mathcal{F}_{\mathrm{disj}}: \forall n \in \omega, \max F_n+1\le \min F_{n+1}\},\\ \mathcal{F}_{\mathrm{int}}:=&\{(F_n) \in \mathcal{F}_{\mathrm{incr}}: \forall n \in \omega, F_n \text{ is an interval}\}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \mathcal{F}_{\mathrm{disj}}:=&\{(F_n) \in (\mathrm{Fin}\setminus \{\emptyset\})^\omega: \forall \{i,j\} \in [\omega]^2, F_i \cap F_j=\emptyset\},\\ \mathcal{F}_{\mathrm{incr}}:=&\{(F_n) \in \mathcal{F}_{\mathrm{disj}}: \forall n \in \omega, \max F_n+1\le \min F_{n+1}\},\\ \mathcal{F}_{\mathrm{int}}:=&\{(F_n) \in \mathcal{F}_{\mathrm{incr}}: \forall n \in \omega, F_n \text{ is an interval}\}. \end{split} \end{align*} $$
In particular,
![]() $\mathcal {F}_{\mathrm {int}}\subseteq \mathcal {F}_{\mathrm {incr}}\subseteq \mathcal {F}_{\mathrm {disj}}$
.
$\mathcal {F}_{\mathrm {int}}\subseteq \mathcal {F}_{\mathrm {incr}}\subseteq \mathcal {F}_{\mathrm {disj}}$
.
We start with some characterizations of generalized density ideals, cf. also Proposition 2.3 and Theorem 5.3.
Proposition 2.1. Let
![]() $\mathcal {I}$
be an ideal. Then the following are equivalent:
$\mathcal {I}$
be an ideal. Then the following are equivalent:
-
(G1)
 $\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
for a sequence
$\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
for a sequence
 $\boldsymbol {\mu }=(\mu _n)$
of lscsms with
$\boldsymbol {\mu }=(\mu _n)$
of lscsms with
 $(\mathrm {supp}(\mu _n)) \in \mathcal {F}_{\mathrm {int}}$
;
$(\mathrm {supp}(\mu _n)) \in \mathcal {F}_{\mathrm {int}}$
; -
(G2)
 $\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
for a sequence
$\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
for a sequence
 $\boldsymbol {\mu }=(\mu _n)$
of lscsms with
$\boldsymbol {\mu }=(\mu _n)$
of lscsms with
 $(\mathrm {supp}(\mu _n)) \in \mathcal {F}_{\mathrm {incr}}$
;
$(\mathrm {supp}(\mu _n)) \in \mathcal {F}_{\mathrm {incr}}$
; -
(G3)
 $\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
for a sequence
$\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
for a sequence
 $\boldsymbol {\mu }=(\mu _n)$
of lscsms with
$\boldsymbol {\mu }=(\mu _n)$
of lscsms with
 $(\mathrm {supp}(\mu _n)) \in \mathcal {F}_{\mathrm {disj}}$
(that is,
$(\mathrm {supp}(\mu _n)) \in \mathcal {F}_{\mathrm {disj}}$
(that is,
 $\mathcal {I}$
is a generalized density ideal); and
$\mathcal {I}$
is a generalized density ideal); and -
(G4)
 $\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
for a sequence
$\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
for a sequence
 $\boldsymbol {\mu }=(\mu _n)$
of bounded lscsms such that
$\boldsymbol {\mu }=(\mu _n)$
of bounded lscsms such that  $$ \begin{align*} \forall k \in \omega,\quad \{n \in \omega: k \in \mathrm{supp}(\mu_n)\} \in \mathrm{Fin}{.} \end{align*} $$
$$ \begin{align*} \forall k \in \omega,\quad \{n \in \omega: k \in \mathrm{supp}(\mu_n)\} \in \mathrm{Fin}{.} \end{align*} $$
Proof. It is clear that (G1)
![]() $\implies $
(G2)
$\implies $
(G2)
![]() $\implies $
(G3)
$\implies $
(G3)
![]() $\implies $
(G4).
$\implies $
(G4).
(G4)
![]() $\implies $
(G3) See [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Proposition 5.4].
$\implies $
(G3) See [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Proposition 5.4].
(G3)
![]() $\implies $
(G1) Suppose that
$\implies $
(G1) Suppose that
![]() $\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
for some sequence
$\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
for some sequence
![]() $\boldsymbol {\mu }=(\mu _n)$
of lscsms such that
$\boldsymbol {\mu }=(\mu _n)$
of lscsms such that
![]() $(S_n) \in \mathcal {F}_{\mathrm {disj}}$
, where
$(S_n) \in \mathcal {F}_{\mathrm {disj}}$
, where
![]() $S_n:=\mathrm {supp}(\mu _n)$
for each n. Note that we can assume without loss of generality that
$S_n:=\mathrm {supp}(\mu _n)$
for each n. Note that we can assume without loss of generality that
![]() $S:=\bigcup _n S_n=\omega $
. Indeed, in the opposite, if
$S:=\bigcup _n S_n=\omega $
. Indeed, in the opposite, if
![]() $S^c$
is finite then it is sufficient to replace
$S^c$
is finite then it is sufficient to replace
![]() $\mu _0(A)$
with
$\mu _0(A)$
with
![]() $\mu _0(A)+|A\cap S^c|$
for all
$\mu _0(A)+|A\cap S^c|$
for all
![]() $A\subseteq \omega $
. Otherwise, let
$A\subseteq \omega $
. Otherwise, let
![]() $(x_n)$
be the infinite increasing enumeration of
$(x_n)$
be the infinite increasing enumeration of
![]() $S^c$
and replace every
$S^c$
and replace every
![]() $\mu _n(A)$
with
$\mu _n(A)$
with
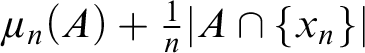 $\mu _n(A)+\frac {1}{n}|A\cap \{x_n\}|$
. This is possible, considering that
$\mu _n(A)+\frac {1}{n}|A\cap \{x_n\}|$
. This is possible, considering that
At this point, let
![]() $(T_n)\in \mathrm {Fin}^\omega $
be the sequence defined recursively as it follows: set
$(T_n)\in \mathrm {Fin}^\omega $
be the sequence defined recursively as it follows: set
![]() $T_0:=[0,\max S_0]$
and, for each
$T_0:=[0,\max S_0]$
and, for each
![]() $n\in \omega $
, set
$n\in \omega $
, set
 $$ \begin{align*} \textstyle T_{n+1}:=\left(\max \bigcup_{i\le n}T_i,\, \max\left(S_{n+1}\cup \bigcup \{S_k: \min S_k \le \max \bigcup_{i\le n}T_i\}\right)\right]. \end{align*} $$
$$ \begin{align*} \textstyle T_{n+1}:=\left(\max \bigcup_{i\le n}T_i,\, \max\left(S_{n+1}\cup \bigcup \{S_k: \min S_k \le \max \bigcup_{i\le n}T_i\}\right)\right]. \end{align*} $$
Observe that
![]() $(T_n)$
is a sequence of (possibly empty) pairwise disjoint finite intervals such that
$(T_n)$
is a sequence of (possibly empty) pairwise disjoint finite intervals such that
![]() $\bigcup _{n}T_n=\omega $
. Moreover, for each
$\bigcup _{n}T_n=\omega $
. Moreover, for each
![]() $n \in \omega $
there exists
$n \in \omega $
there exists
![]() $j=j(n)\in \omega $
with
$j=j(n)\in \omega $
with
![]() $S_n\subseteq T_{j(n)}\cup T_{j(n)+1}$
: indeed, if
$S_n\subseteq T_{j(n)}\cup T_{j(n)+1}$
: indeed, if
![]() $j(n)$
is the minimal integer such that
$j(n)$
is the minimal integer such that
![]() $S_n\cap T_{j(n)}\neq \emptyset $
(so that
$S_n\cap T_{j(n)}\neq \emptyset $
(so that
![]() $T_{j(n)}\neq \emptyset $
and
$T_{j(n)}\neq \emptyset $
and
![]() $\min S_n \le \max T_{j(n)}$
), then
$\min S_n \le \max T_{j(n)}$
), then
 $$ \begin{align*}\textstyle \max(T_{j(n)+1})\geq\max\left(\bigcup\{S_k: \min S_k \le \max \bigcup_{i\le j(n)}T_i\}\right)\geq\max(S_n). \end{align*} $$
$$ \begin{align*}\textstyle \max(T_{j(n)+1})\geq\max\left(\bigcup\{S_k: \min S_k \le \max \bigcup_{i\le j(n)}T_i\}\right)\geq\max(S_n). \end{align*} $$
Let
![]() $(V_n)$
be the biggest subsequence of
$(V_n)$
be the biggest subsequence of
![]() $(T_n)$
with nonempty elements, so that
$(T_n)$
with nonempty elements, so that
![]() $(V_n) \in \mathcal {F}_{\mathrm {int}}$
, and define the sequence
$(V_n) \in \mathcal {F}_{\mathrm {int}}$
, and define the sequence
![]() $\boldsymbol {\nu }=(\nu _n)$
of lscsms by
$\boldsymbol {\nu }=(\nu _n)$
of lscsms by
Note that
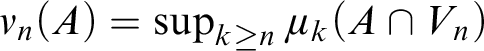 $\nu _n(A)=\sup _{k\geq n}\mu _k(A\cap V_n)$
, since
$\nu _n(A)=\sup _{k\geq n}\mu _k(A\cap V_n)$
, since
![]() $S_k\cap V_n=\emptyset $
whenever
$S_k\cap V_n=\emptyset $
whenever
![]() $k<n$
(indeed
$k<n$
(indeed
 $S_k\subseteq \bigcup _{n\le k} T_n\subseteq \bigcup _{n\le k}V_n$
for all
$S_k\subseteq \bigcup _{n\le k} T_n\subseteq \bigcup _{n\le k}V_n$
for all
![]() $k \in \omega $
). Moreover, it follows by construction that
$k \in \omega $
). Moreover, it follows by construction that
![]() $\text {supp}(\nu _n)=V_n$
for each
$\text {supp}(\nu _n)=V_n$
for each
![]() $n \in \omega $
, hence it is sufficient to show that
$n \in \omega $
, hence it is sufficient to show that
![]() $\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\nu }})$
.
$\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\nu }})$
.
On the one hand, it is clear that if
![]() $\mu _n(A)\to 0$
then
$\mu _n(A)\to 0$
then
 $$ \begin{align*} \textstyle \nu_n(A)=\sup_{k\ge n}\mu_k(A\cap V_n) \le \sup_{k\ge n}\mu_k(A) \to 0, \end{align*} $$
$$ \begin{align*} \textstyle \nu_n(A)=\sup_{k\ge n}\mu_k(A\cap V_n) \le \sup_{k\ge n}\mu_k(A) \to 0, \end{align*} $$
hence
![]() $\mathcal {I}\subseteq \mathrm {Exh}(\varphi _{\boldsymbol {\nu }})$
.
$\mathcal {I}\subseteq \mathrm {Exh}(\varphi _{\boldsymbol {\nu }})$
.
On the other hand, suppose that
![]() $\nu _n(A)\to 0$
and fix
$\nu _n(A)\to 0$
and fix
![]() $\varepsilon>0$
. Then there exists
$\varepsilon>0$
. Then there exists
![]() $n_0\in \omega $
such that
$n_0\in \omega $
such that
![]() for all
for all
![]() $n> n_0$
. Let
$n> n_0$
. Let
![]() $k_0$
be the minimal integer such that
$k_0$
be the minimal integer such that
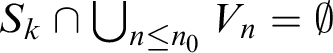 $S_k\cap \bigcup _{n\le n_0}V_n=\emptyset $
for all
$S_k\cap \bigcup _{n\le n_0}V_n=\emptyset $
for all
![]() $k\ge k_0$
. Fix
$k\ge k_0$
. Fix
![]() $k\ge k_0$
and
$k\ge k_0$
and
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $S_k\subseteq V_n\cup V_{n+1}$
(hence, in particular,
$S_k\subseteq V_n\cup V_{n+1}$
(hence, in particular,
![]() $n>n_0$
). We conclude that
$n>n_0$
). We conclude that
 $$ \begin{align*} \begin{split} \mu_k(A)&=\mu_k(A\cap S_k)\leq\mu_k(A\cap (V_n\cup V_{n+1}))\\ &\textstyle \leq\mu_k(A\cap V_n)+\mu_k(A\cap V_{n+1}) \leq\nu_n(A)+\nu_{n+1}(A)\le \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon, \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \mu_k(A)&=\mu_k(A\cap S_k)\leq\mu_k(A\cap (V_n\cup V_{n+1}))\\ &\textstyle \leq\mu_k(A\cap V_n)+\mu_k(A\cap V_{n+1}) \leq\nu_n(A)+\nu_{n+1}(A)\le \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon, \end{split} \end{align*} $$
which shows that
![]() $\mu _k(A)\to 0$
, therefore
$\mu _k(A)\to 0$
, therefore
![]() $\mathrm {Exh}(\varphi _{\boldsymbol {\nu }}) \subseteq \mathcal {I}$
.⊣
$\mathrm {Exh}(\varphi _{\boldsymbol {\nu }}) \subseteq \mathcal {I}$
.⊣
Some additional notations are in order. Given a lscsm
![]() $\varphi $
and a real
$\varphi $
and a real
![]() $\delta>0$
, let
$\delta>0$
, let
![]() $\mathcal {G}_{\varphi ,\delta }$
be the set of sequences of subsets of
$\mathcal {G}_{\varphi ,\delta }$
be the set of sequences of subsets of
![]() $\omega $
with
$\omega $
with
![]() $\varphi $
-value smaller than
$\varphi $
-value smaller than
![]() $\delta $
, that is,
$\delta $
, that is,
Let
![]() $\mathcal {I}$
,
$\mathcal {I}$
,
![]() $\mathcal {J}$
be ideals on
$\mathcal {J}$
be ideals on
![]() $\omega $
and let
$\omega $
and let
![]() $\mathcal {I}^+$
be the family of
$\mathcal {I}^+$
be the family of
![]() $\mathcal {I}$
-positive sets, that is,
$\mathcal {I}$
-positive sets, that is,
![]() $\{A\subseteq \omega : A\notin \mathcal {I}\}$
. Following Solecki and Todorcevic [Reference Solecki and Todorcevic24, p. 1892], we say that a separable metric space X is
$\{A\subseteq \omega : A\notin \mathcal {I}\}$
. Following Solecki and Todorcevic [Reference Solecki and Todorcevic24, p. 1892], we say that a separable metric space X is
![]() $(\mathcal {I}^+,\mathcal {J})$
-calibrated if the following property holds: for each sequence
$(\mathcal {I}^+,\mathcal {J})$
-calibrated if the following property holds: for each sequence
![]() $x=(x_n)$
in X with
$x=(x_n)$
in X with
![]() $\Gamma _x(\mathcal {I}) \neq \emptyset $
, there exists
$\Gamma _x(\mathcal {I}) \neq \emptyset $
, there exists
![]() $A\in \mathcal {I}^+$
such that
$A\in \mathcal {I}^+$
such that
![]() $\{x_n: n \in A\cap B\}$
is bounded for all
$\{x_n: n \in A\cap B\}$
is bounded for all
![]() $B \in \mathcal {J}$
(where
$B \in \mathcal {J}$
(where
![]() $\Gamma _x(\mathcal {I})$
denotes the set of
$\Gamma _x(\mathcal {I})$
denotes the set of
![]() $\mathcal {I}$
-cluster points of x, that is, the set of
$\mathcal {I}$
-cluster points of x, that is, the set of
![]() $\ell \in X$
such that
$\ell \in X$
such that
![]() $\{n \in \omega : x_n \in U\} \notin \mathcal {I}$
for all neighborhoods U of
$\{n \in \omega : x_n \in U\} \notin \mathcal {I}$
for all neighborhoods U of
![]() $\ell $
, cf. [Reference Balcerzak and Leonetti3]).
$\ell $
, cf. [Reference Balcerzak and Leonetti3]).
We continue with some characterizations of density-like ideals, see also [Reference Solecki23, Theorem 4.5].
Proposition 2.2. Let
![]() $\varphi $
be a lscsm and set
$\varphi $
be a lscsm and set
![]() $\mathcal {I}:=\mathrm {Exh}(\varphi )$
. Then the following are equivalent:
$\mathcal {I}:=\mathrm {Exh}(\varphi )$
. Then the following are equivalent:
-
(D1)
 $\textstyle \forall \varepsilon>0, \exists \delta >0, \forall (F_n) \in \mathcal {I}^\omega \cap \mathcal {G}_{\varphi ,\delta }, \exists I \in [\omega ]^\omega , \varphi \left (\bigcup _{i \in I}F_i\right )<\varepsilon $
;
$\textstyle \forall \varepsilon>0, \exists \delta >0, \forall (F_n) \in \mathcal {I}^\omega \cap \mathcal {G}_{\varphi ,\delta }, \exists I \in [\omega ]^\omega , \varphi \left (\bigcup _{i \in I}F_i\right )<\varepsilon $
; -
(D2)
 $\textstyle \forall \varepsilon>0, \exists \delta >0, \forall (F_n) \in \mathrm {Fin}^\omega \cap \mathcal {G}_{\varphi ,\delta }, \exists I \in [\omega ]^\omega , \varphi \left (\bigcup _{i \in I}F_i\right )<\varepsilon $
;
$\textstyle \forall \varepsilon>0, \exists \delta >0, \forall (F_n) \in \mathrm {Fin}^\omega \cap \mathcal {G}_{\varphi ,\delta }, \exists I \in [\omega ]^\omega , \varphi \left (\bigcup _{i \in I}F_i\right )<\varepsilon $
; -
(D3)
 $\textstyle \forall \varepsilon>0, \exists \delta >0, \forall (F_n) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi ,\delta }, \exists I \in [\omega ]^\omega , \varphi \left (\bigcup _{i \in I}F_i\right )<\varepsilon $
(that is,
$\textstyle \forall \varepsilon>0, \exists \delta >0, \forall (F_n) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi ,\delta }, \exists I \in [\omega ]^\omega , \varphi \left (\bigcup _{i \in I}F_i\right )<\varepsilon $
(that is,
 $\mathcal {I}$
is density-like);
$\mathcal {I}$
is density-like); -
(D4)
 $\textstyle \forall \varepsilon>0, \exists \delta >0, \forall (F_n) \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\varphi ,\delta }, \exists I \in [\omega ]^\omega , \varphi \left (\bigcup _{i \in I}F_i\right )<\varepsilon $
; and
$\textstyle \forall \varepsilon>0, \exists \delta >0, \forall (F_n) \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\varphi ,\delta }, \exists I \in [\omega ]^\omega , \varphi \left (\bigcup _{i \in I}F_i\right )<\varepsilon $
; and -
(D5)
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $((\mathrm {Fin}\times \mathrm {Fin})^+, \emptyset \times \mathrm {Fin})$
-calibrated.
$((\mathrm {Fin}\times \mathrm {Fin})^+, \emptyset \times \mathrm {Fin})$
-calibrated.
Proof. It is clear that (D1)
![]() $\implies $
(D2)
$\implies $
(D2)
![]() $\implies $
(D3)
$\implies $
(D3)
![]() $\implies $
(D4).
$\implies $
(D4).
(D3)
![]() $\Longleftrightarrow $
(D5) See [Reference Solecki and Todorcevic24, Lemma 6.7].
$\Longleftrightarrow $
(D5) See [Reference Solecki and Todorcevic24, Lemma 6.7].
(D4)
![]() $\implies $
(D1) See [Reference Solecki and Todorcevic25, Lemma 3.1].⊣
$\implies $
(D1) See [Reference Solecki and Todorcevic25, Lemma 3.1].⊣
To conclude, every density-like ideal is a generalized density ideal, provided that, in addition, it is
![]() $F_\sigma $
.
$F_\sigma $
.
Proposition 2.3. Let
![]() $\mathcal {I}$
be an
$\mathcal {I}$
be an
![]() $F_\sigma $
ideal. Then the following are equivalent:
$F_\sigma $
ideal. Then the following are equivalent:
-
(F1)
 $\mathcal {I}$
is a generalized density ideal;
$\mathcal {I}$
is a generalized density ideal; -
(F2)
 $\mathcal {I}$
is a density-like ideal;
$\mathcal {I}$
is a density-like ideal; -
(F3)
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $((\mathrm {Fin}\times \mathrm {Fin})^+, \emptyset \times \mathrm {Fin})$
-calibrated; and
$((\mathrm {Fin}\times \mathrm {Fin})^+, \emptyset \times \mathrm {Fin})$
-calibrated; and -
(F4)
 $\mathcal {I}=\mathrm {Fin}$
or
$\mathcal {I}=\mathrm {Fin}$
or
 $\mathcal {I}=\mathrm {Fin}\oplus \mathcal {P}(\omega )$
.
$\mathcal {I}=\mathrm {Fin}\oplus \mathcal {P}(\omega )$
.
Proof.
(F1)
![]() $\implies $
(F2) This is obvious.
$\implies $
(F2) This is obvious.
(F2)
![]() $\implies $
(F3) See [Reference Solecki and Todorcevic24, Lemma 6.7].
$\implies $
(F3) See [Reference Solecki and Todorcevic24, Lemma 6.7].
(F3)
![]() $\implies $
(F4) See [Reference Solecki and Todorcevic24, Proposition 6.8(b)].
$\implies $
(F4) See [Reference Solecki and Todorcevic24, Proposition 6.8(b)].
(F4)
![]() $\implies $
(F1) If
$\implies $
(F1) If
![]() $\mathcal {I}=\mathrm {Fin}$
then
$\mathcal {I}=\mathrm {Fin}$
then
![]() $\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
, where
$\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
, where
![]() $\boldsymbol {\mu }=(\mu _n)$
and each
$\boldsymbol {\mu }=(\mu _n)$
and each
![]() $\mu _n$
is the Dirac measure on
$\mu _n$
is the Dirac measure on
![]() $n \in \omega $
. If
$n \in \omega $
. If
![]() $\mathcal {I}=\mathrm {Fin}\oplus \mathcal {P}(\omega )$
is represented on
$\mathcal {I}=\mathrm {Fin}\oplus \mathcal {P}(\omega )$
is represented on
![]() $\omega $
as
$\omega $
as
![]() $\{A\subseteq \omega : A \cap 2\omega \in \mathrm {Fin}\}$
, then
$\{A\subseteq \omega : A \cap 2\omega \in \mathrm {Fin}\}$
, then
![]() $\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
, where
$\mathcal {I}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
, where
![]() $\mu _n$
is the Dirac measure on
$\mu _n$
is the Dirac measure on
![]() $2n$
, for each
$2n$
, for each
![]() $n \in \omega $
.⊣
$n \in \omega $
.⊣
3 Nontall solutions to Question 1
In this section, we provide a positive answer to Question 1 by showing that there exists a nontall density-like ideal which is not a generalized density ideal.
To this aim, given an ideal
![]() $\mathcal {I}\subseteq \mathcal {P}(\omega )$
, define
$\mathcal {I}\subseteq \mathcal {P}(\omega )$
, define
 $$ \begin{align} \widehat{\mathcal{I}}:=h[(\emptyset \times \mathrm{Fin}) \cap (\mathcal{I} \times \emptyset)]. \end{align} $$
$$ \begin{align} \widehat{\mathcal{I}}:=h[(\emptyset \times \mathrm{Fin}) \cap (\mathcal{I} \times \emptyset)]. \end{align} $$
Note that
![]() $(\emptyset \times \mathrm {Fin}) \cap (\mathcal {I} \times \emptyset )$
is an ideal on
$(\emptyset \times \mathrm {Fin}) \cap (\mathcal {I} \times \emptyset )$
is an ideal on
![]() $\omega ^2$
, hence
$\omega ^2$
, hence
![]() $\widehat {\mathcal {I}}$
is an ideal on
$\widehat {\mathcal {I}}$
is an ideal on
![]() $\omega $
. The ideal
$\omega $
. The ideal
![]() $\widehat {\mathcal {I}}$
has been introduced and studied by Oliver in [Reference Oliver20, Definition 2.1], following an idea of Hjorth. It is remarkable that Oliver used these ideals
$\widehat {\mathcal {I}}$
has been introduced and studied by Oliver in [Reference Oliver20, Definition 2.1], following an idea of Hjorth. It is remarkable that Oliver used these ideals
![]() $\widehat {\mathcal {I}}$
to show that, in any model of ZFC, there exist an uncountable family of Borel ideals
$\widehat {\mathcal {I}}$
to show that, in any model of ZFC, there exist an uncountable family of Borel ideals
![]() $\mathcal {J}$
such that the quotient Boolean algebras
$\mathcal {J}$
such that the quotient Boolean algebras
![]() $\mathcal {P}(\omega )/\mathcal {J}$
are pairwise nonisomorphic, see [Reference Oliver20, Theorem 3.2], addressing also a well-known question due to Farah [Reference Farah7].
$\mathcal {P}(\omega )/\mathcal {J}$
are pairwise nonisomorphic, see [Reference Oliver20, Theorem 3.2], addressing also a well-known question due to Farah [Reference Farah7].
Lemma 3.1. Let
![]() $\mathcal {I}$
be an ideal. Then
$\mathcal {I}$
be an ideal. Then
![]() $\widehat {\mathcal {I}}$
is a nontall ideal.
$\widehat {\mathcal {I}}$
is a nontall ideal.
Proof. It is sufficient to see that
![]() $h[\{0\}\times \omega ]$
is an infinite set which does not contain any infinite subset in
$h[\{0\}\times \omega ]$
is an infinite set which does not contain any infinite subset in
![]() $\mathcal {I}$
.⊣
$\mathcal {I}$
.⊣
Here, we show first that if
![]() $\mathcal {I}$
is an analytic P-ideal [density-like, respectively], then so is
$\mathcal {I}$
is an analytic P-ideal [density-like, respectively], then so is
![]() $\widehat {\mathcal {I}}$
; notice that the first claim, with an essentially equivalent proof, can be already found in Oliver’s work [Reference Oliver20, Lemma 3.6], but we repeat it here for the sake of readers’ convenience (e.g., we will make explicit use of the submeasure
$\widehat {\mathcal {I}}$
; notice that the first claim, with an essentially equivalent proof, can be already found in Oliver’s work [Reference Oliver20, Lemma 3.6], but we repeat it here for the sake of readers’ convenience (e.g., we will make explicit use of the submeasure
![]() $\lambda $
defined in (4) also later). Then, we prove that
$\lambda $
defined in (4) also later). Then, we prove that
![]() $\widehat {\mathcal {I}}$
is not a generalized density ideal whenever
$\widehat {\mathcal {I}}$
is not a generalized density ideal whenever
![]() $\mathcal {I}$
is tall.
$\mathcal {I}$
is tall.
Theorem 3.2. Let
![]() $\mathcal {I}$
be an analytic P-ideal. Then
$\mathcal {I}$
be an analytic P-ideal. Then
![]() $\widehat {\mathcal {I}}$
is an analytic P-ideal.
$\widehat {\mathcal {I}}$
is an analytic P-ideal.
Proof. Let
![]() $\varphi $
be a lscsm such that
$\varphi $
be a lscsm such that
![]() $\mathcal {I}=\mathrm {Exh}(\varphi )$
. We may assume that
$\mathcal {I}=\mathrm {Exh}(\varphi )$
. We may assume that
![]() $\mathrm {supp}(\varphi )=\omega $
(indeed, it is easy check that
$\mathrm {supp}(\varphi )=\omega $
(indeed, it is easy check that
![]() $\mathcal {I}=\mathrm {Exh}(\tilde {\varphi })$
, where
$\mathcal {I}=\mathrm {Exh}(\tilde {\varphi })$
, where
![]() $\tilde {\varphi }$
is the lscsm defined by
$\tilde {\varphi }$
is the lscsm defined by
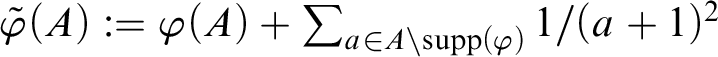 $\tilde {\varphi }(A):=\varphi (A)+\sum _{a \in A\setminus \mathrm {supp}(\varphi )}1/(a+1)^{2}$
for all
$\tilde {\varphi }(A):=\varphi (A)+\sum _{a \in A\setminus \mathrm {supp}(\varphi )}1/(a+1)^{2}$
for all
![]() $A\subseteq \omega $
).
$A\subseteq \omega $
).
Let
![]() $\nu $
be the submeasure defined by
$\nu $
be the submeasure defined by
 $$ \begin{align} \forall B\subseteq \omega^2,\quad \nu(B):=\varphi\left(\left\{m \in \omega: B_{(m)} \neq \emptyset\right\}\right). \end{align} $$
$$ \begin{align} \forall B\subseteq \omega^2,\quad \nu(B):=\varphi\left(\left\{m \in \omega: B_{(m)} \neq \emptyset\right\}\right). \end{align} $$
To conclude the proof, we claim that
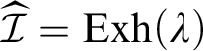 $\widehat {\mathcal {I}}=\mathrm {Exh}(\lambda )$
, where
$\widehat {\mathcal {I}}=\mathrm {Exh}(\lambda )$
, where
![]() $\lambda $
is the submeasure defined by
$\lambda $
is the submeasure defined by
(Note that
![]() $\lambda $
is a lscsm and that
$\lambda $
is a lscsm and that
![]() $\mathrm {supp}(\lambda )=\omega $
.)
$\mathrm {supp}(\lambda )=\omega $
.)
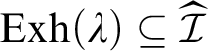 $\mathrm {Exh}(\lambda )\subseteq \widehat {\mathcal {I}}$
: Fix
$\mathrm {Exh}(\lambda )\subseteq \widehat {\mathcal {I}}$
: Fix
![]() $A \in \mathrm {Exh}(\lambda )$
and set
$A \in \mathrm {Exh}(\lambda )$
and set
![]() $B:=h^{-1}[A]$
. Then
$B:=h^{-1}[A]$
. Then
 $$ \begin{align} \textstyle 0=\|A\|_\lambda=\inf_{F \in \mathrm{Fin}}\lambda(A\setminus F)=\inf_{G \in [\omega^2]^{<\omega}}\nu(B\setminus G). \end{align} $$
$$ \begin{align} \textstyle 0=\|A\|_\lambda=\inf_{F \in \mathrm{Fin}}\lambda(A\setminus F)=\inf_{G \in [\omega^2]^{<\omega}}\nu(B\setminus G). \end{align} $$
First, we want to prove that
![]() $B \in \emptyset \times \mathrm {Fin}$
. Indeed, in the opposite, there would exist
$B \in \emptyset \times \mathrm {Fin}$
. Indeed, in the opposite, there would exist
![]() $m \in \omega $
such that
$m \in \omega $
such that
![]() $B_{(m)}\notin \mathrm {Fin}$
. However, we would obtain
$B_{(m)}\notin \mathrm {Fin}$
. However, we would obtain
for every finite set
![]() $G\subseteq \omega ^2$
, which contradicts (5). Secondly, we show that
$G\subseteq \omega ^2$
, which contradicts (5). Secondly, we show that
![]() $B \in \mathcal {I}\times \emptyset $
. Thanks to (5), for every
$B \in \mathcal {I}\times \emptyset $
. Thanks to (5), for every
![]() $\varepsilon>0$
, there exists a finite set
$\varepsilon>0$
, there exists a finite set
![]() $G\subseteq \omega ^2$
such that
$G\subseteq \omega ^2$
such that
![]() $\nu (B\setminus G)<\varepsilon $
. Let
$\nu (B\setminus G)<\varepsilon $
. Let
![]() $F=\{m\in \omega :G_{(m)} \neq \emptyset \}\in \mathrm {Fin}$
. Then
$F=\{m\in \omega :G_{(m)} \neq \emptyset \}\in \mathrm {Fin}$
. Then
 $$ \begin{align*} \varphi\left(\left\{m\in\omega:B_{(m)} \neq \emptyset\right\}\setminus F\right)\leq \varphi\left(\left\{m\in\omega:(B\setminus G)_{(m)} \neq \emptyset\right\}\right)=\nu(B\setminus G)<\varepsilon. \end{align*} $$
$$ \begin{align*} \varphi\left(\left\{m\in\omega:B_{(m)} \neq \emptyset\right\}\setminus F\right)\leq \varphi\left(\left\{m\in\omega:(B\setminus G)_{(m)} \neq \emptyset\right\}\right)=\nu(B\setminus G)<\varepsilon. \end{align*} $$
By the arbitrariness of
![]() $\varepsilon $
, we have
$\varepsilon $
, we have
![]() $B \in \mathcal {I}\times \emptyset $
. To sum up, we have
$B \in \mathcal {I}\times \emptyset $
. To sum up, we have
![]() $B \in (\emptyset \times \mathrm {Fin}) \cap (\mathcal {I}\times \emptyset )$
, so that
$B \in (\emptyset \times \mathrm {Fin}) \cap (\mathcal {I}\times \emptyset )$
, so that
![]() $h^{-1}[\mathrm {Exh}(\lambda )] \subseteq (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}\times \emptyset )$
.
$h^{-1}[\mathrm {Exh}(\lambda )] \subseteq (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}\times \emptyset )$
.
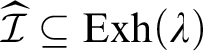 $\widehat {\mathcal {I}}\subseteq \mathrm {Exh}(\lambda )$
: Suppose now that
$\widehat {\mathcal {I}}\subseteq \mathrm {Exh}(\lambda )$
: Suppose now that
![]() $B \in (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}\times \emptyset )$
and fix
$B \in (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}\times \emptyset )$
and fix
![]() $\varepsilon>0$
. Since
$\varepsilon>0$
. Since
![]() $B \in \mathcal {I}\times \emptyset $
, there exists
$B \in \mathcal {I}\times \emptyset $
, there exists
![]() $F\in \mathrm {Fin}$
such that
$F\in \mathrm {Fin}$
such that
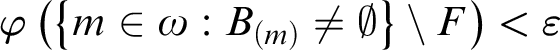 $\varphi \left (\left \{m\in \omega : B_{(m)} \neq \emptyset \right \}\setminus F\right )<\varepsilon $
. However, since
$\varphi \left (\left \{m\in \omega : B_{(m)} \neq \emptyset \right \}\setminus F\right )<\varepsilon $
. However, since
![]() $B \in \emptyset \times \mathrm {Fin}$
, the set
$B \in \emptyset \times \mathrm {Fin}$
, the set
![]() $G:=B \cap (F\times \omega )$
is finite. Hence
$G:=B \cap (F\times \omega )$
is finite. Hence
 $$ \begin{align*} \nu(B\setminus G)=\varphi\left(\left\{m\in\omega:(B\setminus G)_{(m)} \neq \emptyset\right\}\right)=\varphi\left(\left\{m\in\omega:B_{(m)} \neq \emptyset\right\}\setminus F\right)<\varepsilon. \end{align*} $$
$$ \begin{align*} \nu(B\setminus G)=\varphi\left(\left\{m\in\omega:(B\setminus G)_{(m)} \neq \emptyset\right\}\right)=\varphi\left(\left\{m\in\omega:B_{(m)} \neq \emptyset\right\}\setminus F\right)<\varepsilon. \end{align*} $$
Therefore
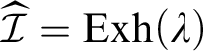 $\widehat {\mathcal {I}}=\mathrm {Exh}(\lambda )$
, which concludes the proof.⊣
$\widehat {\mathcal {I}}=\mathrm {Exh}(\lambda )$
, which concludes the proof.⊣
Remark 3.3. Let us suppose that
![]() $\varphi $
is a nonpathological lscsm (in the sense of Farah [Reference Farah6, Section 1.7]), that is,
$\varphi $
is a nonpathological lscsm (in the sense of Farah [Reference Farah6, Section 1.7]), that is,
 $$ \begin{align*} \textstyle \forall A\subseteq \omega,\quad \varphi(A)=\sup_{\eta \in \mathcal{N}(\varphi)}\eta(A), \end{align*} $$
$$ \begin{align*} \textstyle \forall A\subseteq \omega,\quad \varphi(A)=\sup_{\eta \in \mathcal{N}(\varphi)}\eta(A), \end{align*} $$
where
![]() $\mathcal {N}(\varphi )$
stands for the set of finitely additive measures
$\mathcal {N}(\varphi )$
stands for the set of finitely additive measures
![]() $\eta $
such that
$\eta $
such that
![]() $\eta (V)\le \varphi (V)$
for all
$\eta (V)\le \varphi (V)$
for all
![]() $V\subseteq \omega $
(note that
$V\subseteq \omega $
(note that
![]() $\mathcal {N}(\varphi )\neq \emptyset $
as it contains
$\mathcal {N}(\varphi )\neq \emptyset $
as it contains
![]() $\eta =0$
); strictly related notions have been used in game theory, see [Reference Schmeidler21], and in the context of measure algebras, see [Reference Farah8, Reference Kalton and Roberts13, Reference Talagrand26].
$\eta =0$
); strictly related notions have been used in game theory, see [Reference Schmeidler21], and in the context of measure algebras, see [Reference Farah8, Reference Kalton and Roberts13, Reference Talagrand26].
Then the lscsm
![]() $\lambda $
defined in (4) is nonpathological as well. To this aim, fix
$\lambda $
defined in (4) is nonpathological as well. To this aim, fix
![]() $A\subseteq \omega $
such that
$A\subseteq \omega $
such that
![]() $\lambda (A)\neq 0$
(otherwise the claim is trivial), and recall that
$\lambda (A)\neq 0$
(otherwise the claim is trivial), and recall that
 $$ \begin{align*}\lambda(A)=\nu(h^{-1}[A])=\varphi(M), \text{ where }M:=\{m \in \omega: h^{-1}[A]_{(m)} \neq \emptyset\}. \end{align*} $$
$$ \begin{align*}\lambda(A)=\nu(h^{-1}[A])=\varphi(M), \text{ where }M:=\{m \in \omega: h^{-1}[A]_{(m)} \neq \emptyset\}. \end{align*} $$
In particular, M is nonempty. For each
![]() $m \in M$
, pick
$m \in M$
, pick
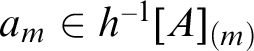 $a_m \in h^{-1}[A]_{(m)}$
. Since
$a_m \in h^{-1}[A]_{(m)}$
. Since
![]() $\varphi $
is nonpathological, there exists a sequence
$\varphi $
is nonpathological, there exists a sequence
![]() $(\eta _n) \in \mathcal {N}(\varphi )^\omega $
such that
$(\eta _n) \in \mathcal {N}(\varphi )^\omega $
such that
![]() $\varphi (M)=\lim _n \eta _n(M)$
. At this point, define
$\varphi (M)=\lim _n \eta _n(M)$
. At this point, define
It is easy to see that each
![]() $\psi _n$
is a finitely additive measure. Moreover, since each
$\psi _n$
is a finitely additive measure. Moreover, since each
![]() $\eta _n$
is pointwise dominated by
$\eta _n$
is pointwise dominated by
![]() $\varphi $
, we have
$\varphi $
, we have
 $$ \begin{align*} \begin{split} \textstyle \forall n \in \omega, \forall V\subseteq \omega,\quad \psi_n(V) &\le \varphi(\{m \in M: (m,a_m) \in h^{-1}[V]\})\\ & \le \varphi(\{m \in M: h^{-1}[V]_{(m)}\neq \emptyset\})\le \lambda(V), \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \textstyle \forall n \in \omega, \forall V\subseteq \omega,\quad \psi_n(V) &\le \varphi(\{m \in M: (m,a_m) \in h^{-1}[V]\})\\ & \le \varphi(\{m \in M: h^{-1}[V]_{(m)}\neq \emptyset\})\le \lambda(V), \end{split} \end{align*} $$
which implies that
![]() $(\psi _n) \in \mathcal {N}(\lambda )^\omega $
. Lastly, we have that
$(\psi _n) \in \mathcal {N}(\lambda )^\omega $
. Lastly, we have that
 $$ \begin{align*} \begin{split} \lambda(A)&\textstyle =\varphi(M)=\lim_{n\to \infty} \eta_n(M)\\ &=\lim_{n \to \infty} \eta_n(\{m \in M: h^{-1}[A]_{(m)} \neq \emptyset\})=\lim_{n\to \infty}\psi_n(A). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \lambda(A)&\textstyle =\varphi(M)=\lim_{n\to \infty} \eta_n(M)\\ &=\lim_{n \to \infty} \eta_n(\{m \in M: h^{-1}[A]_{(m)} \neq \emptyset\})=\lim_{n\to \infty}\psi_n(A). \end{split} \end{align*} $$
This proves that
 $\lambda (A)=\sup _{\psi \in \mathcal {N}(\lambda )}\psi (A)$
, i.e.,
$\lambda (A)=\sup _{\psi \in \mathcal {N}(\lambda )}\psi (A)$
, i.e.,
![]() $\lambda $
is nonpathological.
$\lambda $
is nonpathological.
Now we show that the submeasure
![]() $\lambda $
defined in (4) is density-like provided that
$\lambda $
defined in (4) is density-like provided that
![]() $\varphi $
is density-like (for an alternative shorter proof in the case where
$\varphi $
is density-like (for an alternative shorter proof in the case where
![]() $\mathcal {I}$
is an Erdős-Ulam ideal, see Corollary 4.15).
$\mathcal {I}$
is an Erdős-Ulam ideal, see Corollary 4.15).
Theorem 3.4. Let
![]() $\mathcal {I}$
be a density-like ideal. Then
$\mathcal {I}$
be a density-like ideal. Then
![]() $\widehat {\mathcal {I}}$
is a density-like ideal as well.
$\widehat {\mathcal {I}}$
is a density-like ideal as well.
Proof. Let
![]() $\varphi $
be a density-like lscsm such that
$\varphi $
be a density-like lscsm such that
![]() $\mathcal {I}=\mathrm {Exh}(\varphi )$
and consider the lscsm
$\mathcal {I}=\mathrm {Exh}(\varphi )$
and consider the lscsm
![]() $\lambda $
defined as in the proof of Theorem 3.2. Fix
$\lambda $
defined as in the proof of Theorem 3.2. Fix
![]() $\varepsilon>0$
. By Proposition 2.2, there is
$\varepsilon>0$
. By Proposition 2.2, there is
![]() $\delta =\delta (\varepsilon )>0$
such that for all
$\delta =\delta (\varepsilon )>0$
such that for all
![]() $(E_n) \in \mathrm {Fin}^\omega \cap \mathcal {G}_{\varphi ,\delta }$
there exists
$(E_n) \in \mathrm {Fin}^\omega \cap \mathcal {G}_{\varphi ,\delta }$
there exists
![]() $I \in [\omega ]^\omega $
with
$I \in [\omega ]^\omega $
with
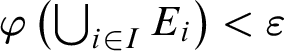 $\varphi \left (\bigcup _{i \in I}E_i\right )<\varepsilon $
. We claim that the same
$\varphi \left (\bigcup _{i \in I}E_i\right )<\varepsilon $
. We claim that the same
![]() $\delta $
witnesses the fact that
$\delta $
witnesses the fact that
![]() $\lambda $
is density-like.
$\lambda $
is density-like.
Fix
![]() $(F_n) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\lambda ,\delta }$
. Define
$(F_n) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\lambda ,\delta }$
. Define
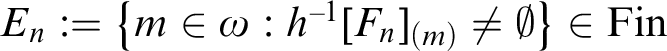 $E_n:=\left \{m \in \omega : h^{-1}[F_n]_{(m)}\neq \emptyset \right \} \in \mathrm {Fin}$
for each
$E_n:=\left \{m \in \omega : h^{-1}[F_n]_{(m)}\neq \emptyset \right \} \in \mathrm {Fin}$
for each
![]() $n \in \omega $
and note that
$n \in \omega $
and note that
 $$ \begin{align*}\varphi(E_n)=\varphi\left(\left\{m \in \omega: h^{-1}[F_n]_{(m)}\neq \emptyset\right\}\right)=\lambda(F_n)<\delta. \end{align*} $$
$$ \begin{align*}\varphi(E_n)=\varphi\left(\left\{m \in \omega: h^{-1}[F_n]_{(m)}\neq \emptyset\right\}\right)=\lambda(F_n)<\delta. \end{align*} $$
Thus,
![]() $(E_n) \in \mathrm {Fin}^\omega \cap \mathcal {G}_{\varphi ,\delta }$
and there exists
$(E_n) \in \mathrm {Fin}^\omega \cap \mathcal {G}_{\varphi ,\delta }$
and there exists
![]() $I \in [\omega ]^\omega $
with
$I \in [\omega ]^\omega $
with
 $\varphi \left (\bigcup _{i \in I}E_i\right )<\varepsilon $
. Then
$\varphi \left (\bigcup _{i \in I}E_i\right )<\varepsilon $
. Then
 $$ \begin{align*}\textstyle \lambda(F)=\varphi(\{m \in \omega: h^{-1}[F]_{(m)} \neq \emptyset\})=\varphi(\bigcup_{i \in I}E_i)<\varepsilon, \end{align*} $$
$$ \begin{align*}\textstyle \lambda(F)=\varphi(\{m \in \omega: h^{-1}[F]_{(m)} \neq \emptyset\})=\varphi(\bigcup_{i \in I}E_i)<\varepsilon, \end{align*} $$
where
![]() $F:=\bigcup _{i \in I}F_i$
. This concludes the proof.⊣
$F:=\bigcup _{i \in I}F_i$
. This concludes the proof.⊣
Theorem 3.5. Let
![]() $\mathcal {I}$
be a tall ideal. Then
$\mathcal {I}$
be a tall ideal. Then
![]() $\widehat {\mathcal {I}}$
is not a generalized density ideal.
$\widehat {\mathcal {I}}$
is not a generalized density ideal.
Proof. Let us suppose that
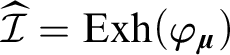 $\widehat {\mathcal {I}}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
, where
$\widehat {\mathcal {I}}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
, where
![]() $\boldsymbol {\mu }=(\mu _n)$
is a sequence of lscsms such that
$\boldsymbol {\mu }=(\mu _n)$
is a sequence of lscsms such that
![]() $(G_n) \in \mathcal {F}_{\mathrm {disj}}$
, where
$(G_n) \in \mathcal {F}_{\mathrm {disj}}$
, where
![]() $G_n:=\mathrm {supp}(\mu _n)$
for each
$G_n:=\mathrm {supp}(\mu _n)$
for each
![]() $n \in \omega $
.
$n \in \omega $
.
Fix a strictly increasing sequence
![]() $(x_n) \in \omega ^\omega $
such that
$(x_n) \in \omega ^\omega $
such that
where
![]() $X:=\{x_k: k \in \omega \}$
(it is easy to see that such sequence exists). It follows that
$X:=\{x_k: k \in \omega \}$
(it is easy to see that such sequence exists). It follows that
![]() $X\notin h[\mathcal {I}\times \emptyset ]$
, hence
$X\notin h[\mathcal {I}\times \emptyset ]$
, hence
 $X\notin \widehat {\mathcal {I}}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
. This implies that there exists
$X\notin \widehat {\mathcal {I}}=\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
. This implies that there exists
![]() $\varepsilon>0$
and a strictly increasing sequence
$\varepsilon>0$
and a strictly increasing sequence
![]() $(m_t)\in \omega ^\omega $
such that
$(m_t)\in \omega ^\omega $
such that
![]() $\mu _{m_t}(X) \ge \varepsilon $
for all
$\mu _{m_t}(X) \ge \varepsilon $
for all
![]() $t \in \omega $
. However, by construction, each
$t \in \omega $
. However, by construction, each
![]() $G_{m_t}$
contains at most one element from X; hence, exactly one since
$G_{m_t}$
contains at most one element from X; hence, exactly one since
![]() $\mu _{m_t}(X)\neq 0$
, let us say
$\mu _{m_t}(X)\neq 0$
, let us say
![]() $\{y_t\}:=G_{m_t} \cap X$
for all
$\{y_t\}:=G_{m_t} \cap X$
for all
![]() $t \in \omega $
. It follows that
$t \in \omega $
. It follows that
![]() $\mu _{m_t}(Z) \not \to 0$
, where Z stands for any infinite subset of
$\mu _{m_t}(Z) \not \to 0$
, where Z stands for any infinite subset of
![]() $Y:=\{y_t: t \in \omega \}$
, therefore
$Y:=\{y_t: t \in \omega \}$
, therefore
![]() $\mathcal {P}(Y) \cap [\omega ]^\omega \cap \mathrm {Exh}(\varphi _{\boldsymbol {\mu }})=\emptyset $
. This implies that every infinite subset of Y does not belong to
$\mathcal {P}(Y) \cap [\omega ]^\omega \cap \mathrm {Exh}(\varphi _{\boldsymbol {\mu }})=\emptyset $
. This implies that every infinite subset of Y does not belong to
![]() $\widehat {\mathcal {I}}$
. Considering that
$\widehat {\mathcal {I}}$
. Considering that
![]() $Y \cap h[\{n\}\times \omega ]$
is finite for all
$Y \cap h[\{n\}\times \omega ]$
is finite for all
![]() $n \in \omega $
, this contradicts the hypothesis that
$n \in \omega $
, this contradicts the hypothesis that
![]() $\mathcal {I}$
is tall.⊣
$\mathcal {I}$
is tall.⊣
As an immediate consequence, we obtain the proof of Theorem 1.3
Proof of Theorem 1.3. Let
![]() $\mathcal {I}_d$
be the ideal of density zero sets, which is a tall generalized density ideal. By Lemma 3.1 and Theorems 3.4 and 3.5, we get that
$\mathcal {I}_d$
be the ideal of density zero sets, which is a tall generalized density ideal. By Lemma 3.1 and Theorems 3.4 and 3.5, we get that
![]() $\widehat {\mathcal {I}}_d$
is a (nontall) density-like ideal which is not a generalized density ideal.⊣
$\widehat {\mathcal {I}}_d$
is a (nontall) density-like ideal which is not a generalized density ideal.⊣
At this point, a natural question would be:
Question 2. How many pairwise nonisomorphic ideals
![]() $\widehat {\mathcal {I}}$
are there, with
$\widehat {\mathcal {I}}$
are there, with
![]() $\mathcal {I}$
tall density-like ideal?
$\mathcal {I}$
tall density-like ideal?
To this aim, given ideals
![]() $\mathcal {I},\mathcal {J}$
on
$\mathcal {I},\mathcal {J}$
on
![]() $\omega $
we say that
$\omega $
we say that
![]() $\mathcal {I}$
is isomorphic to
$\mathcal {I}$
is isomorphic to
![]() $\mathcal {J}$
if there exists a bijection
$\mathcal {J}$
if there exists a bijection
![]() $f: \omega \to \omega $
such that
$f: \omega \to \omega $
such that
![]() $A\in \mathcal {I}$
if and only if
$A\in \mathcal {I}$
if and only if
![]() $f^{-1}[A] \in \mathcal {J}$
for all
$f^{-1}[A] \in \mathcal {J}$
for all
![]() $A\subseteq \omega $
. In addition, we say that
$A\subseteq \omega $
. In addition, we say that
![]() $\mathcal {I}$
is below
$\mathcal {I}$
is below
![]() $\mathcal {J}$
in the Katětov order (written as
$\mathcal {J}$
in the Katětov order (written as
![]() $\mathcal {I}\le _{\mathrm {K}}\mathcal {J}$
) if there exists a function
$\mathcal {I}\le _{\mathrm {K}}\mathcal {J}$
) if there exists a function
![]() $\kappa :\omega \to \omega $
such that
$\kappa :\omega \to \omega $
such that
![]() $A \in \mathcal {I}$
implies
$A \in \mathcal {I}$
implies
![]() $\kappa ^{-1}[A] \in \mathcal {J}$
for all
$\kappa ^{-1}[A] \in \mathcal {J}$
for all
![]() $A\subseteq \omega $
, cf. e.g., [Reference Kwela, Popławski, Swaczyna and Tryba15].
$A\subseteq \omega $
, cf. e.g., [Reference Kwela, Popławski, Swaczyna and Tryba15].
Lastly, we recall that an ideal
![]() $\mathcal {I}$
is called a simple density ideal if there exists a function
$\mathcal {I}$
is called a simple density ideal if there exists a function
![]() $g: \omega \to [0,\infty )$
such that
$g: \omega \to [0,\infty )$
such that
![]() $g(n)\to \infty $
,
$g(n)\to \infty $
,
![]() $n/g(n)\not \to 0$
and
$n/g(n)\not \to 0$
and
 $$ \begin{align*}\mathcal{I}=\mathcal{Z}_g:=\left\{A\subseteq \omega: \lim_{n\to \infty}\frac{|A\cap n|}{g(n)}=0\right\}, \end{align*} $$
$$ \begin{align*}\mathcal{I}=\mathcal{Z}_g:=\left\{A\subseteq \omega: \lim_{n\to \infty}\frac{|A\cap n|}{g(n)}=0\right\}, \end{align*} $$
see [Reference Balcerzak, Das, Filipczak and Swaczyna2, Reference Kwela14, Reference Kwela, Popławski, Swaczyna and Tryba15]. In particular, it has been proved in [Reference Balcerzak, Das, Filipczak and Swaczyna2, Theorem 3.2] that
![]() $\mathcal {Z}_g$
is a density ideal (hence, in particular, a generalized density ideal). It is also evident that
$\mathcal {Z}_g$
is a density ideal (hence, in particular, a generalized density ideal). It is also evident that
![]() $\mathcal {Z}_g$
is tall.
$\mathcal {Z}_g$
is tall.
The next result can be deduced also as an immediate consequence of [Reference Oliver20, Theorem 3.4]; however, the latter one has a different (and seemingly more complicated) proof, hence we present our argument for the sake of completeness.
Theorem 3.6. There are
![]() $2^\omega $
tall density-like ideals
$2^\omega $
tall density-like ideals
![]() $\mathcal {I}$
such that the ideals
$\mathcal {I}$
such that the ideals
![]() $\widehat {\mathcal {I}}$
are pairwise nonisomorphic.
$\widehat {\mathcal {I}}$
are pairwise nonisomorphic.
Proof. Thanks to [Reference Kwela, Popławski, Swaczyna and Tryba15, Theorem 3], there exists a family of simple density ideals
![]() $\{\mathcal {I}_\alpha : \alpha <2^\omega \}$
such that
$\{\mathcal {I}_\alpha : \alpha <2^\omega \}$
such that
![]() $\mathcal {I}_\alpha \not \leq _{\mathrm {K}}\mathcal {I}_\beta $
for all distinct
$\mathcal {I}_\alpha \not \leq _{\mathrm {K}}\mathcal {I}_\beta $
for all distinct
![]() $\alpha ,\beta <2^\omega $
.
$\alpha ,\beta <2^\omega $
.
Hence, given distinct
![]() $\alpha ,\beta <2^{\omega }$
, we claim that
$\alpha ,\beta <2^{\omega }$
, we claim that
![]() $\widehat {\mathcal {I}_\alpha }$
is not isomorphic to
$\widehat {\mathcal {I}_\alpha }$
is not isomorphic to
![]() $\widehat {\mathcal {I}_\beta }$
, i.e., there is no bijection
$\widehat {\mathcal {I}_\beta }$
, i.e., there is no bijection
![]() $f: \omega ^2\to \omega ^2$
such that
$f: \omega ^2\to \omega ^2$
such that
![]() $f[A] \in (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}_\alpha \times \emptyset )$
if and only if
$f[A] \in (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}_\alpha \times \emptyset )$
if and only if
![]() $A \in (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}_\beta \times \emptyset )$
for all
$A \in (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}_\beta \times \emptyset )$
for all
![]() $A\subseteq \omega ^2$
.
$A\subseteq \omega ^2$
.
Suppose that
![]() $f: \omega ^2 \to \omega ^2$
is a bijection and suppose that there exist an infinite set
$f: \omega ^2 \to \omega ^2$
is a bijection and suppose that there exist an infinite set
![]() $A\subseteq \omega $
and
$A\subseteq \omega $
and
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $f[A\times \{0\}]\subseteq \{k\}\times \omega $
. Since
$f[A\times \{0\}]\subseteq \{k\}\times \omega $
. Since
![]() $\mathcal {I}_\beta $
is tall, there is an infinite
$\mathcal {I}_\beta $
is tall, there is an infinite
![]() $B\subseteq A$
such that
$B\subseteq A$
such that
![]() $B\in \mathcal {I}_\beta $
. Thus,
$B\in \mathcal {I}_\beta $
. Thus,
![]() $B\times \{0\}\in (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}_\beta \times \emptyset )$
, but
$B\times \{0\}\in (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}_\beta \times \emptyset )$
, but
![]() $f[B\times \{0\}]\notin (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}_\alpha \times \emptyset )$
as
$f[B\times \{0\}]\notin (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}_\alpha \times \emptyset )$
as
![]() $f[B\times \{0\}]\cap (\{k\}\times \omega )$
is infinite. This implies that the function
$f[B\times \{0\}]\cap (\{k\}\times \omega )$
is infinite. This implies that the function
![]() $g:\omega \to \omega $
defined by
$g:\omega \to \omega $
defined by
![]() $f(n,0) \in \{g(n)\} \times \omega $
for all
$f(n,0) \in \{g(n)\} \times \omega $
for all
![]() $n \in \omega $
is finite-to-one.
$n \in \omega $
is finite-to-one.
Since
![]() $\mathcal {I}_\alpha \not \leq _{\mathrm {K}}\mathcal {I}_\beta $
, there exists a (necessarily infinite) set
$\mathcal {I}_\alpha \not \leq _{\mathrm {K}}\mathcal {I}_\beta $
, there exists a (necessarily infinite) set
![]() $X\in \mathcal {I}_\alpha $
such that
$X\in \mathcal {I}_\alpha $
such that
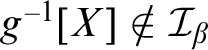 $g^{-1}[X]\notin \mathcal {I}_\beta $
. Define
$g^{-1}[X]\notin \mathcal {I}_\beta $
. Define
![]() $Y:=f[\omega \times \{0\}] \cap (X\times \omega )$
. Note that, since g is finite-to-one, then
$Y:=f[\omega \times \{0\}] \cap (X\times \omega )$
. Note that, since g is finite-to-one, then
![]() $Y\subseteq f[\omega \times \{0\}] \in \emptyset \times \mathrm {Fin}$
. Hence
$Y\subseteq f[\omega \times \{0\}] \in \emptyset \times \mathrm {Fin}$
. Hence
![]() $Y \in (\emptyset \times \mathrm {Fin}) \cap (\mathcal {I}_\alpha \times \emptyset )$
.
$Y \in (\emptyset \times \mathrm {Fin}) \cap (\mathcal {I}_\alpha \times \emptyset )$
.
To conclude the proof, let us suppose for the sake of contradiction that
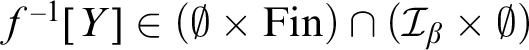 $f^{-1}[Y] \in (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}_\beta \times \emptyset )$
. Hence, in particular,
$f^{-1}[Y] \in (\emptyset \times \mathrm {Fin})\cap (\mathcal {I}_\beta \times \emptyset )$
. Hence, in particular,
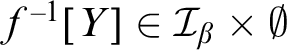 $f^{-1}[Y] \in \mathcal {I}_\beta \times \emptyset $
, that is,
$f^{-1}[Y] \in \mathcal {I}_\beta \times \emptyset $
, that is,
 $$ \begin{align*}Z:=\{n \in\omega: f^{-1}[Y]_{(n)}\neq \emptyset\} \in \mathcal{I}_\beta. \end{align*} $$
$$ \begin{align*}Z:=\{n \in\omega: f^{-1}[Y]_{(n)}\neq \emptyset\} \in \mathcal{I}_\beta. \end{align*} $$
On the other hand, we have
 $$ \begin{align*} \begin{split} Z&=\{n \in \omega: \exists k \in \omega, (n,k) \in f^{-1}[Y]\}=\{n \in \omega: \exists k \in \omega, f(n,k) \in Y\}\\ &=\{n \in \omega: f(n,0) \in Y\}\supseteq \{n \in \omega: g(n) \in X\}=g^{-1}[X] \notin \mathcal{I}_\beta, \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} Z&=\{n \in \omega: \exists k \in \omega, (n,k) \in f^{-1}[Y]\}=\{n \in \omega: \exists k \in \omega, f(n,k) \in Y\}\\ &=\{n \in \omega: f(n,0) \in Y\}\supseteq \{n \in \omega: g(n) \in X\}=g^{-1}[X] \notin \mathcal{I}_\beta, \end{split} \end{align*} $$
where we used that, if
![]() $g(n) \in X$
, then
$g(n) \in X$
, then
![]() $f(n,0) \in \{g(n)\}\times \omega $
and
$f(n,0) \in \{g(n)\}\times \omega $
and
![]() $f(n,0) \in f[\omega \times \{0\}]$
, i.e.,
$f(n,0) \in f[\omega \times \{0\}]$
, i.e.,
![]() $f(n,0) \in Y$
. This completes the proof.⊣
$f(n,0) \in Y$
. This completes the proof.⊣
Thus, we can answer Question 2:
Theorem 3.7. There are
![]() $2^\omega $
nonpathological and pairwise nonisomorphic nontall density-like ideals which are not generalized density ideals.
$2^\omega $
nonpathological and pairwise nonisomorphic nontall density-like ideals which are not generalized density ideals.
4 Tall solutions to Question 1
In the previous Section we have shown that there exists a nontall density-like ideal which is not a generalized density ideal, providing a positive answer to Question 1. Hence, we may ask:
Question 3. Does there exist a tall density-like ideal which is not a generalized density ideal?
In this section, we answer positively also Question 3.
Definition 4.1. A sequence
![]() $\boldsymbol {\mu }=(\mu _n)$
of lscsms is equi-density-like if for all
$\boldsymbol {\mu }=(\mu _n)$
of lscsms is equi-density-like if for all
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $\delta>0$
such that for all
$\delta>0$
such that for all
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $(F_k) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\mu _n,\delta }$
there exists an infinite set
$(F_k) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\mu _n,\delta }$
there exists an infinite set
![]() $I\subseteq \omega $
such that
$I\subseteq \omega $
such that
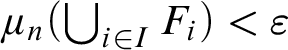 $\mu _n(\bigcup _{i \in I}F_i) < \varepsilon $
.
$\mu _n(\bigcup _{i \in I}F_i) < \varepsilon $
.
In words, each lscsm
![]() $\mu _n$
is density-like and the choice of
$\mu _n$
is density-like and the choice of
![]() $\delta =\delta (\varepsilon )$
is uniform within all
$\delta =\delta (\varepsilon )$
is uniform within all
![]() $\mu _n$
s.
$\mu _n$
s.
Theorem 4.2. Let
![]() $\boldsymbol {\mu }=(\mu _n)$
be a sequence of lscsms with pairwise disjoint supports. Then
$\boldsymbol {\mu }=(\mu _n)$
be a sequence of lscsms with pairwise disjoint supports. Then
![]() $\varphi :=\sup _n\mu _n$
is density-like if and only if
$\varphi :=\sup _n\mu _n$
is density-like if and only if
![]() $\boldsymbol {\mu }$
is equi-density-like.
$\boldsymbol {\mu }$
is equi-density-like.
Proof. Define
![]() $S_n:=\mathrm {supp}(\mu _n)$
for each
$S_n:=\mathrm {supp}(\mu _n)$
for each
![]() $n \in \omega $
.
$n \in \omega $
.
Only If part. Suppose that
![]() $\boldsymbol {\mu }$
is not equi-density-like. Then there exists
$\boldsymbol {\mu }$
is not equi-density-like. Then there exists
![]() $\varepsilon>0$
such that for all
$\varepsilon>0$
such that for all
![]() $\delta>0$
there are
$\delta>0$
there are
![]() $n \in \omega $
and
$n \in \omega $
and
![]() $(F_k) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\mu _n,\delta }$
for which
$(F_k) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\mu _n,\delta }$
for which
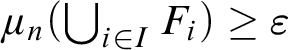 $\mu _n(\bigcup _{i \in I}F_i) \ge \varepsilon $
whenever
$\mu _n(\bigcup _{i \in I}F_i) \ge \varepsilon $
whenever
![]() $I\in [\omega ]^{\omega }$
. We claim that this
$I\in [\omega ]^{\omega }$
. We claim that this
![]() $\varepsilon>0$
witnesses that
$\varepsilon>0$
witnesses that
![]() $\varphi $
is not density-like. To this aim, fix any
$\varphi $
is not density-like. To this aim, fix any
![]() $\delta>0$
and let n and
$\delta>0$
and let n and
![]() $(F_k)$
be as before. Define
$(F_k)$
be as before. Define
![]() $E_k:=F_k \cap S_n$
for all
$E_k:=F_k \cap S_n$
for all
![]() $k \in \omega $
. Then
$k \in \omega $
. Then
![]() $\varphi (E_k)=\mu _n(E_k)<\delta $
and
$\varphi (E_k)=\mu _n(E_k)<\delta $
and
![]() $(E_k) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi , \delta }$
. At the same time, we have
$(E_k) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi , \delta }$
. At the same time, we have
 $$ \begin{align*}\textstyle \forall I \in [\omega]^{\omega}, \quad \varphi\left(\bigcup_{i \in I}E_i\right)=\mu_n\left(\bigcup_{i \in I}E_i\right)=\mu_n\left(\bigcup_{i \in I}F_i\right)\ge \varepsilon. \end{align*} $$
$$ \begin{align*}\textstyle \forall I \in [\omega]^{\omega}, \quad \varphi\left(\bigcup_{i \in I}E_i\right)=\mu_n\left(\bigcup_{i \in I}E_i\right)=\mu_n\left(\bigcup_{i \in I}F_i\right)\ge \varepsilon. \end{align*} $$
Therefore
![]() $\varphi $
is not density-like.
$\varphi $
is not density-like.
If part. Conversely, suppose that
![]() $\boldsymbol {\mu }$
is equi-density-like, and fix
$\boldsymbol {\mu }$
is equi-density-like, and fix
![]() $\varepsilon>0$
. Then there exists a sufficiently small
$\varepsilon>0$
. Then there exists a sufficiently small
![]() such that
such that
 $$ \begin{align} \textstyle \forall n \in \omega, \forall (F_k) \in \mathcal{F}_{\mathrm{disj}} \cap \mathcal{G}_{\mu_n,\delta}, \exists I \in [\omega]^\omega, \mu_n\left(\bigcup_{i \in I}F_i\right)<\frac{\varepsilon}{4}. \end{align} $$
$$ \begin{align} \textstyle \forall n \in \omega, \forall (F_k) \in \mathcal{F}_{\mathrm{disj}} \cap \mathcal{G}_{\mu_n,\delta}, \exists I \in [\omega]^\omega, \mu_n\left(\bigcup_{i \in I}F_i\right)<\frac{\varepsilon}{4}. \end{align} $$
Fix
![]() $(F_k) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi ,\delta }$
and define
$(F_k) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi ,\delta }$
and define
![]() $(T_k) \in \mathrm {Fin}^\omega $
by
$(T_k) \in \mathrm {Fin}^\omega $
by
![]() $T_k:=\{n \in \omega : F_k \cap S_n \neq \emptyset \}$
for all
$T_k:=\{n \in \omega : F_k \cap S_n \neq \emptyset \}$
for all
![]() $k \in \omega $
. At this point, we claim that there exist a sequence of infinite sets
$k \in \omega $
. At this point, we claim that there exist a sequence of infinite sets
![]() $(X_j) \in (\mathrm {Fin}^+)^\omega $
and an increasing sequence
$(X_j) \in (\mathrm {Fin}^+)^\omega $
and an increasing sequence
![]() $(i_j) \in \omega ^\omega $
such that, for all
$(i_j) \in \omega ^\omega $
such that, for all
![]() $j \in \omega $
:
$j \in \omega $
:
-
(i)
 $i_j=\min X_j$
,
$i_j=\min X_j$
, -
(ii)
 $X_{j+1}\subseteq X_j\setminus \{i_j\}$
, and
$X_{j+1}\subseteq X_j\setminus \{i_j\}$
, and -
(iii)
 $\mu _t\left (F^{(j)} \cup \bigcup _{i\in X_{j+1}} F_i\right )<\frac {\varepsilon }{2}$
for each
$\mu _t\left (F^{(j)} \cup \bigcup _{i\in X_{j+1}} F_i\right )<\frac {\varepsilon }{2}$
for each
 $t\in T^{(j)}$
, where
$t\in T^{(j)}$
, where
 $F^{(j)}:=\bigcup _{k\le j} F_{i_k}$
and
$F^{(j)}:=\bigcup _{k\le j} F_{i_k}$
and
 $T^{(j)}:=\bigcup _{k\le j} T_{i_k}$
.
$T^{(j)}:=\bigcup _{k\le j} T_{i_k}$
.
We define these sequences recursively. Start with
![]() $X_0=\omega $
and
$X_0=\omega $
and
![]() $i_0=0$
. Suppose now that
$i_0=0$
. Suppose now that
![]() $X_k$
and
$X_k$
and
![]() $i_k$
have been defined for all
$i_k$
have been defined for all
![]() $k\le j \in \omega $
and satisfy (i)–(iii). If
$k\le j \in \omega $
and satisfy (i)–(iii). If
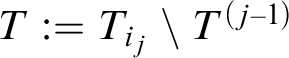 $T:=T_{i_j}\setminus T^{(j-1)}$
is empty, set
$T:=T_{i_j}\setminus T^{(j-1)}$
is empty, set
![]() $X_{j+1}:=X_j\setminus \{i_j\}$
and
$X_{j+1}:=X_j\setminus \{i_j\}$
and
![]() $i_{j+1}:=\min X_{j+1}$
; if
$i_{j+1}:=\min X_{j+1}$
; if
![]() $T\neq \emptyset $
, since
$T\neq \emptyset $
, since
![]() $\mu _n(F_k)\leq \varphi (F_k)<\delta $
for all
$\mu _n(F_k)\leq \varphi (F_k)<\delta $
for all
![]() $n,k\in \omega $
, we can find
$n,k\in \omega $
, we can find
![]() $X_{j+1}\subseteq X_j\setminus \{i_j\}$
such that
$X_{j+1}\subseteq X_j\setminus \{i_j\}$
such that
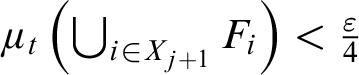 $\mu _t\left (\bigcup _{i \in X_{j+1}}F_i\right )<\frac {\varepsilon }{4}$
for all
$\mu _t\left (\bigcup _{i \in X_{j+1}}F_i\right )<\frac {\varepsilon }{4}$
for all
![]() $t \in T$
; finally, set
$t \in T$
; finally, set
![]() $i_{j+1}:=\min X_{j+1}$
. If
$i_{j+1}:=\min X_{j+1}$
. If
![]() $j\neq 0$
and
$j\neq 0$
and
![]() $t \in T^{(j-1)}$
, it follows by the induction hypothesis that
$t \in T^{(j-1)}$
, it follows by the induction hypothesis that
 $$ \begin{align*}\textstyle \mu_t\left(F^{(j)} \cup \bigcup_{i\in X_{j+1}} F_i\right)\le \mu_t\left(F^{(j-1)} \cup \bigcup_{i\in X_{j}} F_i\right) < \frac{\varepsilon}{2}. \end{align*} $$
$$ \begin{align*}\textstyle \mu_t\left(F^{(j)} \cup \bigcup_{i\in X_{j+1}} F_i\right)\le \mu_t\left(F^{(j-1)} \cup \bigcup_{i\in X_{j}} F_i\right) < \frac{\varepsilon}{2}. \end{align*} $$
On the other hand, if
![]() $j=0$
or
$j=0$
or
![]() $t \in T$
, then
$t \in T$
, then
 $$ \begin{align*}\textstyle \mu_t\left(F^{(j)} \cup \bigcup_{i\in X_{j+1}} F_i\right)\le \mu_t(F_{i_j})+\mu_t\left(\bigcup_{i\in X_{j+1}} F_i\right) < \delta+\frac{\varepsilon}{4}< \frac{\varepsilon}{2}, \end{align*} $$
$$ \begin{align*}\textstyle \mu_t\left(F^{(j)} \cup \bigcup_{i\in X_{j+1}} F_i\right)\le \mu_t(F_{i_j})+\mu_t\left(\bigcup_{i\in X_{j+1}} F_i\right) < \delta+\frac{\varepsilon}{4}< \frac{\varepsilon}{2}, \end{align*} $$
which proves the condition (iii) and completes the induction.
To complete the proof, note that if
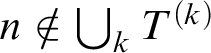 $n \notin \bigcup _k T^{(k)}$
then
$n \notin \bigcup _k T^{(k)}$
then
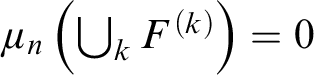 $\mu _n\left (\bigcup _k F^{(k)}\right )=0$
for all
$\mu _n\left (\bigcup _k F^{(k)}\right )=0$
for all
![]() $n \in \omega $
. Moreover, if
$n \in \omega $
. Moreover, if
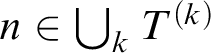 $n \in \bigcup _k T^{(k)}$
then
$n \in \bigcup _k T^{(k)}$
then
 $$ \begin{align*}\textstyle \forall j \in \omega, \quad \mu_n\left(\bigcup_k F^{(k)}\right)\le \mu_n\left(F^{(j)} \cup \bigcup_{i\in X_{j+1}} F_i\right)<\frac{\varepsilon}{2}. \end{align*} $$
$$ \begin{align*}\textstyle \forall j \in \omega, \quad \mu_n\left(\bigcup_k F^{(k)}\right)\le \mu_n\left(F^{(j)} \cup \bigcup_{i\in X_{j+1}} F_i\right)<\frac{\varepsilon}{2}. \end{align*} $$
Thus
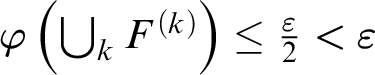 $\varphi \left (\bigcup _k F^{(k)}\right )\le \frac {\varepsilon }{2}<\varepsilon $
, which shows that
$\varphi \left (\bigcup _k F^{(k)}\right )\le \frac {\varepsilon }{2}<\varepsilon $
, which shows that
![]() $\varphi $
is density-like.⊣
$\varphi $
is density-like.⊣
It is worth noting that the above proof works also if
![]() $\boldsymbol {\mu }$
is a sequence of lscsms such that
$\boldsymbol {\mu }$
is a sequence of lscsms such that
![]() $\{n\in \omega :k\in \textrm {supp}(\mu _n)\}$
is finite for all
$\{n\in \omega :k\in \textrm {supp}(\mu _n)\}$
is finite for all
![]() $k\in \omega $
, in the same spirit of [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Proposition 5.4], cf. Proposition 2.1.
$k\in \omega $
, in the same spirit of [Reference Borodulin-Nadzieja, Farkas and Plebanek5, Proposition 5.4], cf. Proposition 2.1.
The aim of the next example is twofold: first of all, it shows that there exist sequences of lscsms that are not equi-density-like (hence, their pointwise supremum is not density-like); secondly, it proves that the ideal
![]() $\mathrm {Exh}(\sup _n \mu _n)$
depends on the sequence of lscsms
$\mathrm {Exh}(\sup _n \mu _n)$
depends on the sequence of lscsms
![]() $(\mu _n)$
, not on the sequence of ideals
$(\mu _n)$
, not on the sequence of ideals
![]() $(\mathrm {Exh}(\mu _n))$
, that is, there are two sequences of lscsms
$(\mathrm {Exh}(\mu _n))$
, that is, there are two sequences of lscsms
![]() $(\mu _n)$
and
$(\mu _n)$
and
![]() $(\nu _n)$
such that
$(\nu _n)$
such that
![]() $\mathrm {Exh}(\mu _n)=\mathrm {Exh}(\nu _n)$
for each
$\mathrm {Exh}(\mu _n)=\mathrm {Exh}(\nu _n)$
for each
![]() $n\in \omega $
and, on the other hand,
$n\in \omega $
and, on the other hand,
![]() $\mathrm {Exh}(\sup _n \mu _n)\neq \mathrm {Exh}(\sup _n \nu _n)$
.
$\mathrm {Exh}(\sup _n \mu _n)\neq \mathrm {Exh}(\sup _n \nu _n)$
.
Example 4.3. Let
![]() $(I_{n,m})_{n,m\in \omega }$
be a sequence of pairwise disjoint finite subsets of
$(I_{n,m})_{n,m\in \omega }$
be a sequence of pairwise disjoint finite subsets of
![]() $\omega $
such that
$\omega $
such that
![]() $|I_{n,m}|=2^{m}$
for each
$|I_{n,m}|=2^{m}$
for each
![]() $n,m\in \omega $
. Moreover, let
$n,m\in \omega $
. Moreover, let
![]() $(\eta _{n,m})_{n,m\in \omega }$
be the sequence of probability measures on
$(\eta _{n,m})_{n,m\in \omega }$
be the sequence of probability measures on
![]() $\omega $
defined by
$\omega $
defined by
 $$ \begin{align*} \forall n,m \in \omega, \forall A\subseteq \omega,\quad \eta_{n,m}(A)=\frac{|A\cap I_{n,m}|}{2^m}. \end{align*} $$
$$ \begin{align*} \forall n,m \in \omega, \forall A\subseteq \omega,\quad \eta_{n,m}(A)=\frac{|A\cap I_{n,m}|}{2^m}. \end{align*} $$
Then, define the sequences of lscsms
![]() $\boldsymbol {\mu }=(\mu _n)$
and
$\boldsymbol {\mu }=(\mu _n)$
and
![]() $\boldsymbol {\nu }=(\nu _n)$
by
$\boldsymbol {\nu }=(\nu _n)$
by
 $$ \begin{align*} \forall n \in \omega,\quad \mu_n=\sup_{m \in \omega}\eta_{n,m} \,\,\,\text{ and }\,\,\, \nu_n=\sup_{M \in [\omega]^{n+1}}\sum_{m \in M} \eta_{n,m}, \end{align*} $$
$$ \begin{align*} \forall n \in \omega,\quad \mu_n=\sup_{m \in \omega}\eta_{n,m} \,\,\,\text{ and }\,\,\, \nu_n=\sup_{M \in [\omega]^{n+1}}\sum_{m \in M} \eta_{n,m}, \end{align*} $$
where the suprema are meant in the pointwise order.
On the one hand, it is easy to see that
![]() $\|A\|_{\mu _n}=0$
if and only if
$\|A\|_{\mu _n}=0$
if and only if
![]() $\|A\|_{\nu _n}=0$
, so that
$\|A\|_{\nu _n}=0$
, so that
![]() $\mathrm {Exh}(\mu _n)$
and
$\mathrm {Exh}(\mu _n)$
and
![]() $\mathrm {Exh}(\nu _n)$
are density ideals and they coincide for each
$\mathrm {Exh}(\nu _n)$
are density ideals and they coincide for each
![]() $n \in \omega $
.
$n \in \omega $
.
On the other hand,
![]() $\mathrm {Exh}(\sup _n \mu _n)=\mathrm {Exh}(\sup _{n,m}\eta _{n,m})$
is a density ideal (hence, in particular, it is a density-like ideal), and it is not equal to
$\mathrm {Exh}(\sup _n \mu _n)=\mathrm {Exh}(\sup _{n,m}\eta _{n,m})$
is a density ideal (hence, in particular, it is a density-like ideal), and it is not equal to
![]() $\mathrm {Exh}(\sup _n \nu _n)$
. Indeed, we will prove that
$\mathrm {Exh}(\sup _n \nu _n)$
. Indeed, we will prove that
![]() $\mathrm {Exh}(\sup _n \nu _n)$
is not density-like. Thanks to Theorem 4.2, this is equivalent to show that
$\mathrm {Exh}(\sup _n \nu _n)$
is not density-like. Thanks to Theorem 4.2, this is equivalent to show that
![]() $\boldsymbol {\nu }$
is not equi-density-like.
$\boldsymbol {\nu }$
is not equi-density-like.
To this aim, put
![]() $\varepsilon =1$
and fix any
$\varepsilon =1$
and fix any
![]() $\delta>0$
. There is
$\delta>0$
. There is
![]() $k\in \omega $
such that
$k\in \omega $
such that
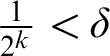 $\frac {1}{2^k}<\delta $
. We will find a sequence
$\frac {1}{2^k}<\delta $
. We will find a sequence
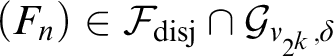 $(F_n) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\nu _{2^k},\delta }$
such that
$(F_n) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\nu _{2^k},\delta }$
such that
 $\nu _{2^k}(\bigcup _{i \in I}F_i) \geq \varepsilon $
for each infinite
$\nu _{2^k}(\bigcup _{i \in I}F_i) \geq \varepsilon $
for each infinite
![]() $I\subseteq \omega $
. For each
$I\subseteq \omega $
. For each
![]() $n \in \omega $
, fix a subset
$n \in \omega $
, fix a subset
![]() $F_n\subseteq I_{2^k,k+n}$
such that
$F_n\subseteq I_{2^k,k+n}$
such that
![]() $|F_n|=2^n$
. Note that
$|F_n|=2^n$
. Note that
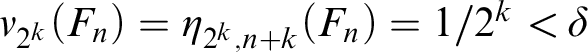 $\nu _{2^k}(F_n)=\eta _{2^k,n+k}(F_n)=1/2^{k}<\delta $
for all
$\nu _{2^k}(F_n)=\eta _{2^k,n+k}(F_n)=1/2^{k}<\delta $
for all
![]() $n \in \omega $
. Therefore
$n \in \omega $
. Therefore
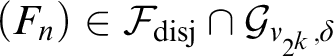 $(F_n) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\nu _{2^k},\delta }$
. Lastly, fix an infinite set
$(F_n) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\nu _{2^k},\delta }$
. Lastly, fix an infinite set
![]() $I \subseteq \omega $
and a subset
$I \subseteq \omega $
and a subset
![]() $M\subseteq I$
such that
$M\subseteq I$
such that
![]() $|M|=2^k+1$
. Then
$|M|=2^k+1$
. Then
 $$ \begin{align*}\nu_{2^k}\left(\bigcup_{i \in I}F_i\right) \geq \nu_{2^k}\left(\bigcup_{i \in M}F_{i}\right) \ge \sum_{m \in M}\eta_{2^k,k+m}\left(\bigcup_{i \in M}F_{i}\right) =\sum_{m \in M}\eta_{2^k,k+m}(F_m)>1, \end{align*} $$
$$ \begin{align*}\nu_{2^k}\left(\bigcup_{i \in I}F_i\right) \geq \nu_{2^k}\left(\bigcup_{i \in M}F_{i}\right) \ge \sum_{m \in M}\eta_{2^k,k+m}\left(\bigcup_{i \in M}F_{i}\right) =\sum_{m \in M}\eta_{2^k,k+m}(F_m)>1, \end{align*} $$
which proves that
![]() $\boldsymbol {\nu }$
is not equi-density-like.
$\boldsymbol {\nu }$
is not equi-density-like.
Definition 4.4. A lscsm
![]() $\varphi $
is strongly-density-like if there is a constant
$\varphi $
is strongly-density-like if there is a constant
![]() $c= c(\varphi )>0$
such that, for all
$c= c(\varphi )>0$
such that, for all
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $(F_k) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi ,c \varepsilon }$
, there exists an infinite set
$(F_k) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi ,c \varepsilon }$
, there exists an infinite set
![]() $I \subseteq \omega $
such that
$I \subseteq \omega $
such that
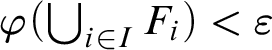 $\varphi (\bigcup _{i \in I}F_i) < \varepsilon $
.
$\varphi (\bigcup _{i \in I}F_i) < \varepsilon $
.
Remark 4.5. Observe that if
![]() $\boldsymbol {\mu }$
is a sequence of lscsms with pairwise disjoint finite supports, then
$\boldsymbol {\mu }$
is a sequence of lscsms with pairwise disjoint finite supports, then
![]() $\varphi _{\boldsymbol {\mu }}=\sup _n \mu _n$
is strongly-density-like with any constant
$\varphi _{\boldsymbol {\mu }}=\sup _n \mu _n$
is strongly-density-like with any constant
![]() $c(\varphi _{\boldsymbol {\mu }})<1$
. Thus, if
$c(\varphi _{\boldsymbol {\mu }})<1$
. Thus, if
![]() $\mathcal {I}$
is a generalized density ideal, then there is a strongly-density-like lscsm
$\mathcal {I}$
is a generalized density ideal, then there is a strongly-density-like lscsm
![]() $\varphi $
with
$\varphi $
with
![]() $\varphi $
with
$\varphi $
with
![]() $\mathcal {I}=\mathrm {Exh}(\varphi )$
.
$\mathcal {I}=\mathrm {Exh}(\varphi )$
.
In the following example we show that there exist density-like lscsms which are not strongly-density-like, cf. also Section 6.
Example 4.6. Let
![]() $h: \omega ^2 \to \omega $
be the bijection defined in (1). For each
$h: \omega ^2 \to \omega $
be the bijection defined in (1). For each
![]() $n \in \omega $
define
$n \in \omega $
define
![]() $X_n:=h^{-1}[\{n\}\times \omega ]$
, so that
$X_n:=h^{-1}[\{n\}\times \omega ]$
, so that
![]() $\{X_n\}$
is a partition of
$\{X_n\}$
is a partition of
![]() $\omega $
into infinite sets. Define
$\omega $
into infinite sets. Define
![]() $a_k:=1/(k+2)!$
for each
$a_k:=1/(k+2)!$
for each
![]() $k \in \omega $
and note that
$k \in \omega $
and note that
![]() $a_k\to 0$
as
$a_k\to 0$
as
![]() $k\to +\infty $
and
$k\to +\infty $
and
![]() $a_{k-1}>(k+1)a_k$
for all
$a_{k-1}>(k+1)a_k$
for all
![]() $k>0$
. Moreover, set
$k>0$
. Moreover, set
![]() $\varphi :=\sup _n \mu _n$
, where
$\varphi :=\sup _n \mu _n$
, where
![]() $(\mu _n)$
is the sequence of lscsms given by
$(\mu _n)$
is the sequence of lscsms given by
We claim that
![]() $\varphi $
is a density-like lscsm which is not strongly-density-like.
$\varphi $
is a density-like lscsm which is not strongly-density-like.
First, we show that
![]() $\varphi $
is not strongly-density-like. To this aim, fix an arbitrary constant
$\varphi $
is not strongly-density-like. To this aim, fix an arbitrary constant
![]() $c>0$
and a positive integer k such that
$c>0$
and a positive integer k such that
![]() . Then, set
. Then, set
![]() $\varepsilon :=(k+1)a_k$
and
$\varepsilon :=(k+1)a_k$
and
![]() $F_n:=\{h^{-1}(k,n)\}$
for each
$F_n:=\{h^{-1}(k,n)\}$
for each
![]() $n \in \omega $
. It follows that
$n \in \omega $
. It follows that
 $$ \begin{align*}\textstyle \forall n\in \omega,\quad \varphi(F_n)=\mu_k(F_k)=a_k< \frac{(k+1)a_k}{k}\le c\varepsilon, \end{align*} $$
$$ \begin{align*}\textstyle \forall n\in \omega,\quad \varphi(F_n)=\mu_k(F_k)=a_k< \frac{(k+1)a_k}{k}\le c\varepsilon, \end{align*} $$
hence
![]() $(F_n) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi ,c\varepsilon }$
. On the other hand, for each infinite set
$(F_n) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi ,c\varepsilon }$
. On the other hand, for each infinite set
![]() $I\subseteq \omega $
, we have
$I\subseteq \omega $
, we have
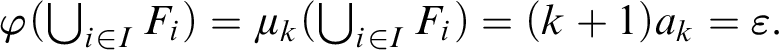 $ \varphi (\bigcup _{i \in I}F_i)= \mu _k(\bigcup _{i \in I}F_i)=(k+1)a_k=\varepsilon. $
$ \varphi (\bigcup _{i \in I}F_i)= \mu _k(\bigcup _{i \in I}F_i)=(k+1)a_k=\varepsilon. $
Now let us show that
![]() $\varphi $
is density-like. Fix
$\varphi $
is density-like. Fix
![]() $\varepsilon>0$
and define
$\varepsilon>0$
and define
![]() $\delta :=a_k$
, where k is an integer such that
$\delta :=a_k$
, where k is an integer such that
![]() $(k+1)a_k<\varepsilon $
. Fix also
$(k+1)a_k<\varepsilon $
. Fix also
![]() $(F_k) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi ,\delta }$
. Note that
$(F_k) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi ,\delta }$
. Note that
 $F_k \cap \bigcup _{n\le k-1}X_n=\emptyset $
for each
$F_k \cap \bigcup _{n\le k-1}X_n=\emptyset $
for each
![]() $k \in \omega $
: indeed
$k \in \omega $
: indeed
 $$ \begin{align*}\textstyle \forall x \in \bigcup_{n\le k-1}X_{n},\quad \varphi(\{x\}) \ge a_{k-1}> (k+1)a_{k} \ge a_{k} =\delta. \end{align*} $$
$$ \begin{align*}\textstyle \forall x \in \bigcup_{n\le k-1}X_{n},\quad \varphi(\{x\}) \ge a_{k-1}> (k+1)a_{k} \ge a_{k} =\delta. \end{align*} $$
Therefore
 $$ \begin{align*} \forall I \in [\omega]^\omega,\quad \varphi\left(\bigcup_{i \in I}F_{i}\right)\le \varphi\left(\bigcup_{n\ge k}X_n\right)=\sup_{k\ge n} \mu_k(X_k)=(k+1)a_k<\varepsilon, \end{align*} $$
$$ \begin{align*} \forall I \in [\omega]^\omega,\quad \varphi\left(\bigcup_{i \in I}F_{i}\right)\le \varphi\left(\bigcup_{n\ge k}X_n\right)=\sup_{k\ge n} \mu_k(X_k)=(k+1)a_k<\varepsilon, \end{align*} $$
concluding the proof.
Proposition 4.7. Fix
![]() $q \in [1,\infty )$
. Then the set of strongly-density-like lscsms is q-convex, that is, for each strongly-density-like lscsms
$q \in [1,\infty )$
. Then the set of strongly-density-like lscsms is q-convex, that is, for each strongly-density-like lscsms
![]() $\varphi _1,\ldots ,\varphi _k$
and
$\varphi _1,\ldots ,\varphi _k$
and
![]() $a_1,\ldots ,a_k \in [0,1]$
with
$a_1,\ldots ,a_k \in [0,1]$
with
 $\sum _{i\le k} a_i=1$
, the lscsm
$\sum _{i\le k} a_i=1$
, the lscsm
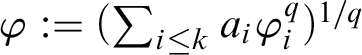 $ \varphi :=(\sum _{i\le k}a_i \varphi _i^q)^{1/q} $
is strongly-density-like. In addition, a witnessing constant of
$ \varphi :=(\sum _{i\le k}a_i \varphi _i^q)^{1/q} $
is strongly-density-like. In addition, a witnessing constant of
![]() $\varphi $
is
$\varphi $
is
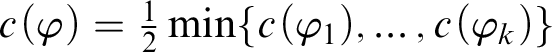 $c(\varphi )=\frac {1}{2}\min \{c(\varphi _1),\ldots ,c(\varphi _k)\}$
.
$c(\varphi )=\frac {1}{2}\min \{c(\varphi _1),\ldots ,c(\varphi _k)\}$
.
Proof. Let
![]() $\varphi _1,\ldots ,\varphi _k$
be strongly-density-like lscsms, fix
$\varphi _1,\ldots ,\varphi _k$
be strongly-density-like lscsms, fix
![]() $a_1,\ldots ,a_k \in [0,1]$
with
$a_1,\ldots ,a_k \in [0,1]$
with
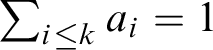 $\sum _{i\le k} a_i=1$
, and define the lscsm
$\sum _{i\le k} a_i=1$
, and define the lscsm
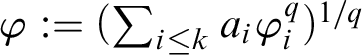 $\varphi :=(\sum _{i\le k}a_i \varphi _i^q)^{1/q}$
. Set
$\varphi :=(\sum _{i\le k}a_i \varphi _i^q)^{1/q}$
. Set
 $c:=\frac {1}{2}\min _{i\le k}c(\varphi _i)$
, so that
$c:=\frac {1}{2}\min _{i\le k}c(\varphi _i)$
, so that
![]() $2c$
is a witnessing constant for each
$2c$
is a witnessing constant for each
![]() $\varphi _i$
.
$\varphi _i$
.
Fix
![]() $\varepsilon>0$
and a sequence
$\varepsilon>0$
and a sequence
![]() $(F_j) \in \mathcal {F}_{\mathrm {disj}}\cap \mathcal {G}_{\varphi ,c\varepsilon }$
. For each
$(F_j) \in \mathcal {F}_{\mathrm {disj}}\cap \mathcal {G}_{\varphi ,c\varepsilon }$
. For each
![]() $j \in \omega $
and
$j \in \omega $
and
![]() $i \in \{1,\ldots ,k\}$
define the integer
$i \in \{1,\ldots ,k\}$
define the integer
![]() $ z_{i,j}:=\left \lfloor \varphi _i(F_j)/c\varepsilon \right \rfloor. $
Note that
$ z_{i,j}:=\left \lfloor \varphi _i(F_j)/c\varepsilon \right \rfloor. $
Note that
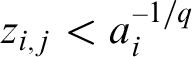 $z_{i,j}<a_i^{-1/q}$
, indeed
$z_{i,j}<a_i^{-1/q}$
, indeed
 $$ \begin{align*}\textstyle \forall i=1,\ldots,k,\quad c\varepsilon>\varphi(F_j)\ge a_i^{1/q}\varphi_i(F_j) \ge a_i^{1/q}z_{i,j}c\varepsilon. \end{align*} $$
$$ \begin{align*}\textstyle \forall i=1,\ldots,k,\quad c\varepsilon>\varphi(F_j)\ge a_i^{1/q}\varphi_i(F_j) \ge a_i^{1/q}z_{i,j}c\varepsilon. \end{align*} $$
Considering that
 $L:=\prod _{i=1}^k (\omega \cap [0,a_i^{-1/q}))$
is finite, there exists
$L:=\prod _{i=1}^k (\omega \cap [0,a_i^{-1/q}))$
is finite, there exists
![]() $\ell =(\ell _1,\ldots ,\ell _k) \in L$
and an infinite set
$\ell =(\ell _1,\ldots ,\ell _k) \in L$
and an infinite set
![]() $J\subseteq \omega $
such that
$J\subseteq \omega $
such that
![]() $z_{i,j}=\ell _i$
for all
$z_{i,j}=\ell _i$
for all
![]() $i =1,\ldots ,k$
and
$i =1,\ldots ,k$
and
![]() $j \in J$
.
$j \in J$
.
At this point, observe that
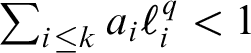 $\sum _{i\le k}a_i\ell _i^q<1$
, indeed
$\sum _{i\le k}a_i\ell _i^q<1$
, indeed
 $$ \begin{align*} \sum_{i\le k}a_i(c\varepsilon\ell_i)^q=\sum_{i\le k}a_i(c\varepsilon z_{i,\min J})^q\le \sum_{i\le k}a_i\varphi_i(F_{\min J})^q=\varphi(F_{\min J})^q < (c\varepsilon)^q. \end{align*} $$
$$ \begin{align*} \sum_{i\le k}a_i(c\varepsilon\ell_i)^q=\sum_{i\le k}a_i(c\varepsilon z_{i,\min J})^q\le \sum_{i\le k}a_i\varphi_i(F_{\min J})^q=\varphi(F_{\min J})^q < (c\varepsilon)^q. \end{align*} $$
Since each
![]() $\varphi _i$
is strongly-density-like with witnessing constant
$\varphi _i$
is strongly-density-like with witnessing constant
![]() $2c$
, we have that
$2c$
, we have that
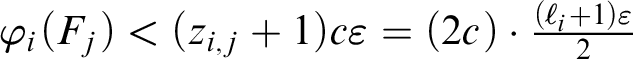 $\varphi _i(F_j)<(z_{i,j}+1)c\varepsilon =(2c)\cdot \frac {(\ell _i+1)\varepsilon }{2}$
for all
$\varphi _i(F_j)<(z_{i,j}+1)c\varepsilon =(2c)\cdot \frac {(\ell _i+1)\varepsilon }{2}$
for all
![]() $j \in J$
. Hence there exists an infinite set
$j \in J$
. Hence there exists an infinite set
![]() $T\subseteq J$
such that
$T\subseteq J$
such that
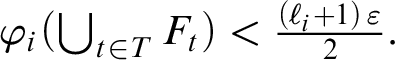 $ \varphi _i(\bigcup _{t \in T}F_t)<\frac {(\ell _i+1)\,\varepsilon }{2}. $
for all
$ \varphi _i(\bigcup _{t \in T}F_t)<\frac {(\ell _i+1)\,\varepsilon }{2}. $
for all
![]() $i=1,\ldots ,k$
.
$i=1,\ldots ,k$
.
Thanks to Minkowski’s inequality, we conclude that
 $$ \begin{align*} \textstyle \varphi(\bigcup_{t \in T}F_t)<\frac{\varepsilon}{2}\left(\sum_{i\le k}a_i (\ell_i+1)^q\right)^{1/q}\le \frac{\varepsilon}{2}\left(\left(\sum_{i\le k}a_i\ell_i^q\right)^{1/q}+1\right)<\varepsilon, \end{align*} $$
$$ \begin{align*} \textstyle \varphi(\bigcup_{t \in T}F_t)<\frac{\varepsilon}{2}\left(\sum_{i\le k}a_i (\ell_i+1)^q\right)^{1/q}\le \frac{\varepsilon}{2}\left(\left(\sum_{i\le k}a_i\ell_i^q\right)^{1/q}+1\right)<\varepsilon, \end{align*} $$
which proves that
![]() $\varphi $
is strongly-density-like.⊣
$\varphi $
is strongly-density-like.⊣
Definition 4.8. An ideal
![]() $\mathcal {I}$
is said to be a
$\mathcal {I}$
is said to be a
![]() $\mathrm {DL}$
-ideal if it is isomorphic to some
$\mathrm {DL}$
-ideal if it is isomorphic to some
![]() $\mathrm {Exh}(\psi )$
, where
$\mathrm {Exh}(\psi )$
, where
![]() $\psi =\psi (\boldsymbol {\varphi },q,a,S)$
is a lscsm on
$\psi =\psi (\boldsymbol {\varphi },q,a,S)$
is a lscsm on
![]() $\omega ^2$
defined by
$\omega ^2$
defined by
 $$ \begin{align} \forall A\subseteq \omega^2,\quad \psi(A):=\sup_{n \in \omega}\,(\sum_{k \in S_n}a_k \varphi_k^{q_n}(A_{(k)}))^{1/q_n}, \end{align} $$
$$ \begin{align} \forall A\subseteq \omega^2,\quad \psi(A):=\sup_{n \in \omega}\,(\sum_{k \in S_n}a_k \varphi_k^{q_n}(A_{(k)}))^{1/q_n}, \end{align} $$
where
![]() $\boldsymbol {\varphi }=(\varphi _n)$
is a sequence a strongly-density-like lscsms on
$\boldsymbol {\varphi }=(\varphi _n)$
is a sequence a strongly-density-like lscsms on
![]() $\omega $
,
$\omega $
,
![]() $q=(q_n)$
is a sequence in
$q=(q_n)$
is a sequence in
![]() $[1,\infty )$
, and
$[1,\infty )$
, and
![]() $a=(a_n) \in [0,1]^\omega $
and
$a=(a_n) \in [0,1]^\omega $
and
![]() $S=(S_n) \in \mathcal {F}_{\mathrm {disj}}$
are sequences such that
$S=(S_n) \in \mathcal {F}_{\mathrm {disj}}$
are sequences such that
![]() $\sum _{k \in S_n}a_k=1$
for all
$\sum _{k \in S_n}a_k=1$
for all
![]() $n \in \omega $
.
$n \in \omega $
.
For the rest of this section, it may be helpful to take in mind the following example of DL-ideals.
Example 4.9. Fix a strictly increasing sequence
![]() $(\iota _n)$
of nonnegative integers such that
$(\iota _n)$
of nonnegative integers such that
![]() $\iota _0:=0$
and
$\iota _0:=0$
and
![]() $\lim _n |I_n|=\infty $
, where
$\lim _n |I_n|=\infty $
, where
![]() $I_n:=[\iota _n,\iota _{n+1})$
for all
$I_n:=[\iota _n,\iota _{n+1})$
for all
![]() $n \in \omega $
. In particular, thanks to Remark 4.5, the map
$n \in \omega $
. In particular, thanks to Remark 4.5, the map
![]() $\mathcal {P}(\omega ) \to [0,\infty ]$
defined by
$\mathcal {P}(\omega ) \to [0,\infty ]$
defined by
![]() $S\mapsto \sup _m |S\cap I_m|/|I_m|$
is a strongly-density-like lscsm. It follows that
$S\mapsto \sup _m |S\cap I_m|/|I_m|$
is a strongly-density-like lscsm. It follows that
![]() $\mathcal {I}:=\{h[A]: A \in \mathrm {Exh}(\psi )\}$
is a DL-ideal, where
$\mathcal {I}:=\{h[A]: A \in \mathrm {Exh}(\psi )\}$
is a DL-ideal, where
![]() $\psi : \omega ^2 \to [0,\infty ]$
is the lscsm defined by
$\psi : \omega ^2 \to [0,\infty ]$
is the lscsm defined by
 $$ \begin{align*}\forall A\subseteq \omega^2, \quad \psi(A):=\sup_{n \in \omega} \left(\frac{1}{|I_n|}\sum_{k \in I_n}\sup_{m\in \omega} \frac{|A_{(k)}\cap I_m|}{|I_m|}\right). \end{align*} $$
$$ \begin{align*}\forall A\subseteq \omega^2, \quad \psi(A):=\sup_{n \in \omega} \left(\frac{1}{|I_n|}\sum_{k \in I_n}\sup_{m\in \omega} \frac{|A_{(k)}\cap I_m|}{|I_m|}\right). \end{align*} $$
As it will be shown below in Corollary 4.21, the above ideal provides an affirmative answer to Question 3.
Remark 4.10. It is not difficult to see that, if
![]() $\psi =\psi (\boldsymbol {\varphi },q,a,S)$
is a lscsm on
$\psi =\psi (\boldsymbol {\varphi },q,a,S)$
is a lscsm on
![]() $\omega ^2$
as in (7) such that q is the constant sequence
$\omega ^2$
as in (7) such that q is the constant sequence
![]() $(1)$
and each
$(1)$
and each
![]() $\varphi _n$
is nonpathological, then
$\varphi _n$
is nonpathological, then
![]() $\psi $
is nonpathological as well. For each lscsm
$\psi $
is nonpathological as well. For each lscsm
![]() $\phi $
on
$\phi $
on
![]() $\omega $
and for each
$\omega $
and for each
![]() $k \in \omega $
, let
$k \in \omega $
, let
![]() $\tilde {\phi }^{(k)}$
be the lscsm on
$\tilde {\phi }^{(k)}$
be the lscsm on
![]() $\omega ^2$
defined by
$\omega ^2$
defined by
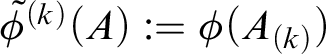 $\tilde {\phi }^{(k)}(A):=\phi (A_{(k)})$
for all
$\tilde {\phi }^{(k)}(A):=\phi (A_{(k)})$
for all
![]() $A\subseteq \omega ^2$
. Then, with the same notation of Remark 3.3, we know that
$A\subseteq \omega ^2$
. Then, with the same notation of Remark 3.3, we know that
 $$ \begin{align*} \forall A\subseteq \omega^2, \forall k \in \omega,\quad \varphi_k(A_{(k)})=\sup_{\eta \in \mathcal{N}(\varphi_k)}\eta(A_{(k)}) =\sup_{\tilde{\eta}^{(k)} \in \mathcal{N}_k(\varphi_k)}\tilde{\eta}^{(k)}(A), \end{align*} $$
$$ \begin{align*} \forall A\subseteq \omega^2, \forall k \in \omega,\quad \varphi_k(A_{(k)})=\sup_{\eta \in \mathcal{N}(\varphi_k)}\eta(A_{(k)}) =\sup_{\tilde{\eta}^{(k)} \in \mathcal{N}_k(\varphi_k)}\tilde{\eta}^{(k)}(A), \end{align*} $$
where
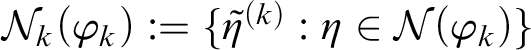 $\mathcal {N}_k(\varphi _k):=\{\tilde {\eta }^{(k)}: \eta \in \mathcal {N}(\varphi _k)\}$
(note that, if
$\mathcal {N}_k(\varphi _k):=\{\tilde {\eta }^{(k)}: \eta \in \mathcal {N}(\varphi _k)\}$
(note that, if
![]() $k\neq k^\prime $
, then measures in
$k\neq k^\prime $
, then measures in
![]() $\mathcal {N}_k(\varphi _k)$
have disjoint supports from measures in
$\mathcal {N}_k(\varphi _k)$
have disjoint supports from measures in
![]() $\mathcal {N}_{k^\prime }(\varphi _{k^\prime })$
). Let
$\mathcal {N}_{k^\prime }(\varphi _{k^\prime })$
). Let
![]() $\tilde {\mathcal {N}}(\psi )$
be the set of finitely additive measures on
$\tilde {\mathcal {N}}(\psi )$
be the set of finitely additive measures on
![]() $\omega ^2$
which are pointwise dominated by
$\omega ^2$
which are pointwise dominated by
![]() $\psi $
. Then
$\psi $
. Then
 $$ \begin{align*} \begin{split} \forall A\subseteq \omega^2,\quad \sup_{\tilde{\eta} \in \tilde{\mathcal{N}}(\psi)}\tilde{\eta}(A)&\le \psi(A)=\sup_{n \in \omega} \sum_{k \in S_n} a_k \sup_{\tilde{\eta}^{(k)} \in \mathcal{N}_k(\varphi_k)} \tilde{\eta}^{(k)}(A)\\ &=\sup_{n \in \omega} \sup_{\substack{\tilde{\eta}^{(k)} \in \mathcal{N}_k(\varphi_k), \\ \text{ with }k \in S_n}} \sum_{k \in S_n} a_k \tilde{\eta}^{(k)}(A) \le \sup_{\tilde{\eta} \in \tilde{\mathcal{N}}(\psi)}\tilde{\eta}(A), \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \forall A\subseteq \omega^2,\quad \sup_{\tilde{\eta} \in \tilde{\mathcal{N}}(\psi)}\tilde{\eta}(A)&\le \psi(A)=\sup_{n \in \omega} \sum_{k \in S_n} a_k \sup_{\tilde{\eta}^{(k)} \in \mathcal{N}_k(\varphi_k)} \tilde{\eta}^{(k)}(A)\\ &=\sup_{n \in \omega} \sup_{\substack{\tilde{\eta}^{(k)} \in \mathcal{N}_k(\varphi_k), \\ \text{ with }k \in S_n}} \sum_{k \in S_n} a_k \tilde{\eta}^{(k)}(A) \le \sup_{\tilde{\eta} \in \tilde{\mathcal{N}}(\psi)}\tilde{\eta}(A), \end{split} \end{align*} $$
where the last inequality is justified by the fact that each
 $\sum _{k \in S_n} a_k \tilde {\eta }^{(k)}$
is finitely additive measure which is dominated by
$\sum _{k \in S_n} a_k \tilde {\eta }^{(k)}$
is finitely additive measure which is dominated by
![]() $\psi $
. Therefore
$\psi $
. Therefore
![]() $\psi $
is nonpathological.
$\psi $
is nonpathological.
Remark 4.11. Each generalized density ideal is a
![]() $\mathrm {DL}$
-ideal. Indeed, let
$\mathrm {DL}$
-ideal. Indeed, let
![]() $\boldsymbol {\mu }=(\mu _n)$
be a sequence of lscsms with pairwise disjoint finite supports such that
$\boldsymbol {\mu }=(\mu _n)$
be a sequence of lscsms with pairwise disjoint finite supports such that
![]() $\mathcal {I}=\mathrm {Exh}(\sup _n \mu _n)$
. Moreover, let
$\mathcal {I}=\mathrm {Exh}(\sup _n \mu _n)$
. Moreover, let
![]() $h: \omega ^2 \to \omega $
be the bijection defined in (1) and
$h: \omega ^2 \to \omega $
be the bijection defined in (1) and
![]() $f: \omega ^2 \to \omega $
be a bijection such that
$f: \omega ^2 \to \omega $
be a bijection such that
Then it suffices to set
![]() $\boldsymbol {\varphi }=(\varphi _n)$
, where
$\boldsymbol {\varphi }=(\varphi _n)$
, where
![]() $\varphi _n(A)=\sup _{m\in \omega }\mu _{h(n,m)}(f[\{n\}\times A])$
for all
$\varphi _n(A)=\sup _{m\in \omega }\mu _{h(n,m)}(f[\{n\}\times A])$
for all
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $A\subseteq \omega $
,
$A\subseteq \omega $
,
![]() $q=(1)$
,
$q=(1)$
,
![]() $a=(1)$
, and
$a=(1)$
, and
![]() $S=(\{n\})$
. It follows that each
$S=(\{n\})$
. It follows that each
![]() $\varphi _n$
is strongly-density-like (cf. Remark 4.5) and that
$\varphi _n$
is strongly-density-like (cf. Remark 4.5) and that
![]() $\mathcal {I}$
is isomorphic to
$\mathcal {I}$
is isomorphic to
![]() $\mathrm {Exh}(\psi )$
, where
$\mathrm {Exh}(\psi )$
, where
![]() $\psi =\psi (\boldsymbol {\varphi },q,a,S)$
is the lscsm on
$\psi =\psi (\boldsymbol {\varphi },q,a,S)$
is the lscsm on
![]() $\omega ^2$
defined as in (7).
$\omega ^2$
defined as in (7).
Proposition 4.12. Let
![]() $\mathcal {I}$
be an Erdős–Ulam ideal. Then
$\mathcal {I}$
be an Erdős–Ulam ideal. Then
![]() $\widehat {\mathcal {I}}$
is a
$\widehat {\mathcal {I}}$
is a
![]() $\mathrm {DL}$
-ideal.
$\mathrm {DL}$
-ideal.
Proof. By [Reference Farah6, Example 1.2.3(d), Theorem 1.13.3(a), and Lemma 1.13.9(Z3)], there is a sequence
![]() $\boldsymbol {\mu }=(\mu _n)$
of probability measures on
$\boldsymbol {\mu }=(\mu _n)$
of probability measures on
![]() $\omega $
such that
$\omega $
such that
![]() $\mathcal {I}=\mathrm {Exh}(\sup _n \mu _n)$
, and
$\mathcal {I}=\mathrm {Exh}(\sup _n \mu _n)$
, and
![]() $(M_n) \in \mathcal {F}_{\mathrm {disj}}$
, where
$(M_n) \in \mathcal {F}_{\mathrm {disj}}$
, where
![]() $M_n:=\mathrm {supp}(\mu _n)$
for each
$M_n:=\mathrm {supp}(\mu _n)$
for each
![]() $n \in \omega $
. Then
$n \in \omega $
. Then
![]() $\widehat {\mathcal {I}}$
is isomorphic to the ideal
$\widehat {\mathcal {I}}$
is isomorphic to the ideal
![]() $\mathrm {Exh}(\nu )$
on
$\mathrm {Exh}(\nu )$
on
![]() $\omega ^2$
, where
$\omega ^2$
, where
![]() $\nu $
is the lscsm defined by
$\nu $
is the lscsm defined by
 $$ \begin{align*}\textstyle \forall A\subseteq \omega^2,\quad \nu(A)=\sup_{n\in \omega} \mu_n(\{k \in \omega: A_{(k)}\neq \emptyset\}), \end{align*} $$
$$ \begin{align*}\textstyle \forall A\subseteq \omega^2,\quad \nu(A)=\sup_{n\in \omega} \mu_n(\{k \in \omega: A_{(k)}\neq \emptyset\}), \end{align*} $$
cf. (3) in the proof of Theorem 3.2.
To conclude the proof, we show that
![]() $\nu =\psi $
, for some
$\nu =\psi $
, for some
![]() $\psi =\psi (\boldsymbol {\varphi },q,a,S)$
. To this aim, let
$\psi =\psi (\boldsymbol {\varphi },q,a,S)$
. To this aim, let
![]() $\boldsymbol {\varphi }$
be the constant sequence
$\boldsymbol {\varphi }$
be the constant sequence
![]() $(\varphi )$
, where
$(\varphi )$
, where
![]() $\varphi $
is the strongly-density-like lscsm defined by
$\varphi $
is the strongly-density-like lscsm defined by
![]() $\varphi (\emptyset )=0$
and
$\varphi (\emptyset )=0$
and
![]() $\varphi (S)=1$
for all nonempty
$\varphi (S)=1$
for all nonempty
![]() $S\subseteq \omega $
. Let also q be the constant sequence
$S\subseteq \omega $
. Let also q be the constant sequence
![]() $(1)$
,
$(1)$
,
![]() $S_n=M_n$
, and
$S_n=M_n$
, and
![]() $a_k:=\sup _n \mu _n(\{k\})$
for all
$a_k:=\sup _n \mu _n(\{k\})$
for all
![]() $n \in \omega $
(note that
$n \in \omega $
(note that
![]() $\sum _{k\in S_n}a_k=1$
for all
$\sum _{k\in S_n}a_k=1$
for all
![]() $n \in \omega $
). It follows that
$n \in \omega $
). It follows that
 $$ \begin{align*} \forall A\subseteq \omega^2,\quad \psi(A)=\sup_{n \in \omega}\sum_{k \in S_n}a_k \varphi(A_{(k)})=\sup_{n \in \omega}\mu_n(\{k \in S_n: A_{(k)}\neq \emptyset\})=\nu(A). \end{align*} $$
$$ \begin{align*} \forall A\subseteq \omega^2,\quad \psi(A)=\sup_{n \in \omega}\sum_{k \in S_n}a_k \varphi(A_{(k)})=\sup_{n \in \omega}\mu_n(\{k \in S_n: A_{(k)}\neq \emptyset\})=\nu(A). \end{align*} $$
Therefore
![]() $\widehat {\mathcal {I}}$
is a
$\widehat {\mathcal {I}}$
is a
![]() $\mathrm {DL}$
-ideal.⊣
$\mathrm {DL}$
-ideal.⊣
Theorem 4.13. Let
![]() $\psi =\psi (\boldsymbol {\varphi },q,a,S)$
be a lscsm on
$\psi =\psi (\boldsymbol {\varphi },q,a,S)$
be a lscsm on
![]() $\omega ^2$
as in (7) such that
$\omega ^2$
as in (7) such that
![]() $\inf _n c(\varphi _n)>0$
. Then
$\inf _n c(\varphi _n)>0$
. Then
![]() $\psi $
is a density-like lscsm.
$\psi $
is a density-like lscsm.
Proof. For each
![]() $k \in \omega $
define the lscsm
$k \in \omega $
define the lscsm
![]() $\tilde {\varphi }_k$
on
$\tilde {\varphi }_k$
on
![]() $\omega ^2$
by
$\omega ^2$
by
 $$ \begin{align*} \forall A\subseteq \omega^2,\quad \tilde{\varphi}_k(A)=\varphi_k(A_{(k)}). \end{align*} $$
$$ \begin{align*} \forall A\subseteq \omega^2,\quad \tilde{\varphi}_k(A)=\varphi_k(A_{(k)}). \end{align*} $$
Then each
![]() $\tilde {\varphi }_k$
is a strongly-density-like lscsm such that
$\tilde {\varphi }_k$
is a strongly-density-like lscsm such that
![]() $c(\tilde {\varphi }_k)=c(\varphi _k)$
. Moreover, for each
$c(\tilde {\varphi }_k)=c(\varphi _k)$
. Moreover, for each
![]() $n \in \omega $
, define the lscsm
$n \in \omega $
, define the lscsm
![]() $\psi _n$
by
$\psi _n$
by
 $$ \begin{align*}\forall A\subseteq \omega^2,\quad \psi_n(A)=\left(\sum_{k \in S_n}a_k\tilde{\varphi}_k(A)^{q_n}\right)^{1/q_n}. \end{align*} $$
$$ \begin{align*}\forall A\subseteq \omega^2,\quad \psi_n(A)=\left(\sum_{k \in S_n}a_k\tilde{\varphi}_k(A)^{q_n}\right)^{1/q_n}. \end{align*} $$
It follows by Proposition 4.7 that each lscsm
![]() $\psi _n$
is strongly-density-like with witnessing constant
$\psi _n$
is strongly-density-like with witnessing constant
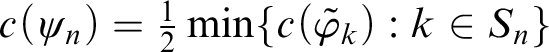 $c(\psi _n)=\frac {1}{2}\min \{c(\tilde {\varphi }_k): k \in S_n\}$
. Since
$c(\psi _n)=\frac {1}{2}\min \{c(\tilde {\varphi }_k): k \in S_n\}$
. Since
![]() $\inf _n c(\varphi _n)>0$
, we have also
$\inf _n c(\varphi _n)>0$
, we have also
![]() $\inf _n c(\psi _n)>0$
, which implies that
$\inf _n c(\psi _n)>0$
, which implies that
![]() $(\psi _n)$
is equi-density-like sequence of lscsms with pairwise disjoint supports (indeed
$(\psi _n)$
is equi-density-like sequence of lscsms with pairwise disjoint supports (indeed
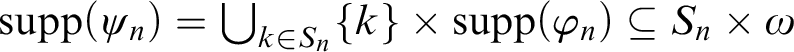 $\mathrm {supp}(\psi _n)=\bigcup _{k \in S_n}\{k\}\times \mathrm {supp}(\varphi _n)\subseteq S_n \times \omega $
). Therefore, thanks to Theorem 4.2,
$\mathrm {supp}(\psi _n)=\bigcup _{k \in S_n}\{k\}\times \mathrm {supp}(\varphi _n)\subseteq S_n \times \omega $
). Therefore, thanks to Theorem 4.2,
![]() $\psi =\sup _n \psi _n$
is density-like.⊣
$\psi =\sup _n \psi _n$
is density-like.⊣
The following corollary is immediate.
Corollary 4.14. Let
![]() $\mathcal {I}$
be a
$\mathcal {I}$
be a
![]() $\mathrm {DL}$
-ideal isomorphic to
$\mathrm {DL}$
-ideal isomorphic to
![]() $\mathrm {Exh}(\psi )$
, where
$\mathrm {Exh}(\psi )$
, where
![]() $\psi =\psi (\boldsymbol {\varphi },q,a,S)$
is a lscsm on
$\psi =\psi (\boldsymbol {\varphi },q,a,S)$
is a lscsm on
![]() $\omega ^2$
such that
$\omega ^2$
such that
![]() $\boldsymbol {\varphi }$
is a constant sequence. Then
$\boldsymbol {\varphi }$
is a constant sequence. Then
![]() $\mathcal {I}$
is density-like.
$\mathcal {I}$
is density-like.
Note that, as it follows from the proof of Proposition 4.12, if
![]() $\mathcal {I}$
is an Erdős–Ulam ideal, then
$\mathcal {I}$
is an Erdős–Ulam ideal, then
![]() $\widehat {\mathcal {I}}$
is isomorphic to
$\widehat {\mathcal {I}}$
is isomorphic to
![]() $\mathrm {Exh}(\psi )$
, where
$\mathrm {Exh}(\psi )$
, where
![]() $\psi =\psi (\boldsymbol {\varphi },q,a,S)$
is a lscsm such that
$\psi =\psi (\boldsymbol {\varphi },q,a,S)$
is a lscsm such that
![]() $\boldsymbol {\varphi }$
is a constant sequence. Therefore, thanks to Corollary 4.14, we obtain:
$\boldsymbol {\varphi }$
is a constant sequence. Therefore, thanks to Corollary 4.14, we obtain:
Corollary 4.15. Let
![]() $\mathcal {I}$
be an Erdős–Ulam ideal. Then
$\mathcal {I}$
be an Erdős–Ulam ideal. Then
![]() $\widehat {\mathcal {I}}$
is a density-like ideal.
$\widehat {\mathcal {I}}$
is a density-like ideal.
Note that Corollary 4.15 is also a consequence of Theorem 3.4; however, the proof of the latter uses Proposition 2.2, which in turn relies on [Reference Solecki and Todorcevic25, Lemma 3.1].
Note that, thanks to Proposition 4.7,
![]() $\psi $
is the pointwise supremum of strongly-density-like lscsms. Now we show that, under some additional hypotheses, the exhaustive ideal generated by
$\psi $
is the pointwise supremum of strongly-density-like lscsms. Now we show that, under some additional hypotheses, the exhaustive ideal generated by
![]() $\psi $
is tall.
$\psi $
is tall.
Proposition 4.16. Let
![]() $\psi =\psi (\boldsymbol {\varphi },q,a,S)$
be a lscsm on
$\psi =\psi (\boldsymbol {\varphi },q,a,S)$
be a lscsm on
![]() $\omega ^2$
as in (7) and assume that
$\omega ^2$
as in (7) and assume that
![]() $\mathrm {Exh}(\varphi _n)$
is tall for all
$\mathrm {Exh}(\varphi _n)$
is tall for all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $M:=\sup _{n,k}\varphi _n(\{k\})<\infty $
, and
$M:=\sup _{n,k}\varphi _n(\{k\})<\infty $
, and
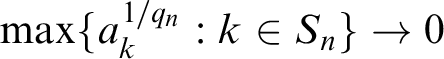 $\max \{a_k^{1/q_n}: k \in S_n\}\to 0$
as
$\max \{a_k^{1/q_n}: k \in S_n\}\to 0$
as
![]() $n\to \infty $
. Then
$n\to \infty $
. Then
![]() $\mathrm {Exh}(\psi )$
is tall.
$\mathrm {Exh}(\psi )$
is tall.
Proof. Let
![]() $A\subseteq \omega ^2$
be an infinite set. If
$A\subseteq \omega ^2$
be an infinite set. If
![]() $A \in \mathrm {Exh}(\psi )$
then the claim is trivial. Hence, suppose hereafter that
$A \in \mathrm {Exh}(\psi )$
then the claim is trivial. Hence, suppose hereafter that
![]() $A\in \mathrm {Exh}(\psi )^+$
, that is,
$A\in \mathrm {Exh}(\psi )^+$
, that is,
 $$ \begin{align} \|A\|_\psi=\inf_{F \in [\omega^2]^{<\omega}}\,\sup_{n \in \omega}\,\left(\sum_{k \in S_n}a_k \varphi_k^{q_n}(A_{(k)}\setminus F)\right)^{1/q_n}>0. \end{align} $$
$$ \begin{align} \|A\|_\psi=\inf_{F \in [\omega^2]^{<\omega}}\,\sup_{n \in \omega}\,\left(\sum_{k \in S_n}a_k \varphi_k^{q_n}(A_{(k)}\setminus F)\right)^{1/q_n}>0. \end{align} $$
Now, suppose that there exists
![]() $m \in \omega $
such that
$m \in \omega $
such that
![]() $A_{(m)}$
is infinite. Since
$A_{(m)}$
is infinite. Since
![]() $\mathrm {Exh}(\varphi _m)$
is tall, there exists an infinite set
$\mathrm {Exh}(\varphi _m)$
is tall, there exists an infinite set
![]() $B\subseteq A\cap (\{m\}\times \omega )$
such that
$B\subseteq A\cap (\{m\}\times \omega )$
such that
![]() $B_{(m)} \in \mathrm {Exh}(\varphi _m)$
. It follows by the definition of
$B_{(m)} \in \mathrm {Exh}(\varphi _m)$
. It follows by the definition of
![]() $\psi $
that
$\psi $
that
![]() $B \in \mathrm {Exh}(\psi )$
.
$B \in \mathrm {Exh}(\psi )$
.
Otherwise
![]() $A \in (\emptyset \times \mathrm {Fin}) \cap \mathrm {Exh}(\psi )^+$
, so that
$A \in (\emptyset \times \mathrm {Fin}) \cap \mathrm {Exh}(\psi )^+$
, so that
![]() $A_{(m)}$
is finite for each
$A_{(m)}$
is finite for each
![]() $m \in \omega $
. Let B be an infinite subset of A such that
$m \in \omega $
. Let B be an infinite subset of A such that
![]() $|B \cap \bigcup _{m \in S_n}A_{(m)}|\le 1$
for all
$|B \cap \bigcup _{m \in S_n}A_{(m)}|\le 1$
for all
![]() $n \in \omega $
(which exists, otherwise A itself would be finite, contradicting (8)). It follows that
$n \in \omega $
(which exists, otherwise A itself would be finite, contradicting (8)). It follows that
 $$ \begin{align*} \begin{split} \|B\|_\psi&\le \inf_{m\in \omega} \|B\setminus \left(\bigcup_{i\le m}S_i \times \omega\right)\|_{\psi} \le \inf_{m \in \omega}\psi\left( B\setminus \left(\bigcup_{i\le m}S_i \times \omega\right)\right)\\ &\le \inf_{m \in \omega} \sup_{n\ge m}\,\left(\sum_{k \in S_n}a_k \varphi_k^{q_n}(B_{(k)})\right)^{1/q_n} \\ &\le M \, \limsup_{n\to\infty} \max\{a_k^{1/q_n}: k \in S_n\} =0. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \|B\|_\psi&\le \inf_{m\in \omega} \|B\setminus \left(\bigcup_{i\le m}S_i \times \omega\right)\|_{\psi} \le \inf_{m \in \omega}\psi\left( B\setminus \left(\bigcup_{i\le m}S_i \times \omega\right)\right)\\ &\le \inf_{m \in \omega} \sup_{n\ge m}\,\left(\sum_{k \in S_n}a_k \varphi_k^{q_n}(B_{(k)})\right)^{1/q_n} \\ &\le M \, \limsup_{n\to\infty} \max\{a_k^{1/q_n}: k \in S_n\} =0. \end{split} \end{align*} $$
Therefore
![]() $B \in \mathrm {Exh}(\psi )$
, concluding the proof.⊣
$B \in \mathrm {Exh}(\psi )$
, concluding the proof.⊣
As a consequence, we obtain that:
Corollary 4.17. Let
![]() $\psi =\psi (\boldsymbol {\varphi },q,a,S)$
be a lscsm on
$\psi =\psi (\boldsymbol {\varphi },q,a,S)$
be a lscsm on
![]() $\omega ^2$
as in (7) and assume that
$\omega ^2$
as in (7) and assume that
![]() $\boldsymbol {\varphi }$
is the constant sequence
$\boldsymbol {\varphi }$
is the constant sequence
![]() $(\varphi )$
, q is a bounded sequence,
$(\varphi )$
, q is a bounded sequence,
![]() $\mathrm {Exh}(\varphi )$
is tall, and
$\mathrm {Exh}(\varphi )$
is tall, and
![]() $\lim _n a_n=0$
. Then
$\lim _n a_n=0$
. Then
![]() $\mathrm {Exh}(\psi )$
is tall.
$\mathrm {Exh}(\psi )$
is tall.
Proof. First of all, we have
![]() $\sup _n \varphi (\{n\})<\infty $
: indeed, in the opposite case, there would exist an increasing sequence
$\sup _n \varphi (\{n\})<\infty $
: indeed, in the opposite case, there would exist an increasing sequence
![]() $(n_k)$
in
$(n_k)$
in
![]() $\omega $
such that
$\omega $
such that
![]() $\varphi (\{n_k\}) \ge k$
for all k and every infinite subset of
$\varphi (\{n_k\}) \ge k$
for all k and every infinite subset of
![]() $\{n_k: k \in \omega \}$
would not belong to
$\{n_k: k \in \omega \}$
would not belong to
![]() $\mathrm {Exh}(\varphi )$
, contradicting the hypothesis that
$\mathrm {Exh}(\varphi )$
, contradicting the hypothesis that
![]() $\mathrm {Exh}(\varphi )$
is tall. Moreover, since
$\mathrm {Exh}(\varphi )$
is tall. Moreover, since
![]() $Q:=\sup _n q_n <\infty $
, we obtain
$Q:=\sup _n q_n <\infty $
, we obtain
 $$ \begin{align*}\textstyle \lim_n \max \{a_k^{1/q_n}: k \in S_n\}\le \lim_n \max \{a_k^{1/Q}: k \in S_n\} =0. \end{align*} $$
$$ \begin{align*}\textstyle \lim_n \max \{a_k^{1/q_n}: k \in S_n\}\le \lim_n \max \{a_k^{1/Q}: k \in S_n\} =0. \end{align*} $$
The claim follows by Proposition 4.16.⊣
Theorem 4.18. Let
![]() $\psi =\psi (\boldsymbol {\varphi }, q, a, S)$
be a lscsm on
$\psi =\psi (\boldsymbol {\varphi }, q, a, S)$
be a lscsm on
![]() $\omega ^2$
as in (7) such that
$\omega ^2$
as in (7) such that
and
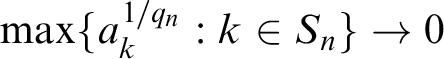 $\max \{a_k^{1/q_n}: k \in S_n\} \to 0$
as
$\max \{a_k^{1/q_n}: k \in S_n\} \to 0$
as
![]() $n\to \infty $
. Then
$n\to \infty $
. Then
![]() $\mathrm {Exh}(\psi )$
is not a generalized density ideal.
$\mathrm {Exh}(\psi )$
is not a generalized density ideal.
Proof. Suppose for the sake of contradiction that
![]() $\mathrm {Exh}(\psi )=\mathrm {Exh}(\sup _n \mu _n)$
, where
$\mathrm {Exh}(\psi )=\mathrm {Exh}(\sup _n \mu _n)$
, where
![]() $(\mu _n)$
is a sequence of lscsms on
$(\mu _n)$
is a sequence of lscsms on
![]() $\omega ^2$
with finite pairwise disjoint supports and set
$\omega ^2$
with finite pairwise disjoint supports and set
![]() $M_n:=\mathrm {supp}(\mu _n)$
for each n (note that
$M_n:=\mathrm {supp}(\mu _n)$
for each n (note that
![]() $M_n \subseteq \omega ^2$
). It follows by the standing assumptions that there exists a sequence
$M_n \subseteq \omega ^2$
). It follows by the standing assumptions that there exists a sequence
![]() $(F_n) \in \mathcal {F}_{\mathrm {incr}}$
such that
$(F_n) \in \mathcal {F}_{\mathrm {incr}}$
such that
 $$ \begin{align} \forall n \in \omega,\quad \varphi_n(F_n) \ge \frac{\inf_{k \in \omega}\| \omega\|_{\varphi_k}}{2} \,\,\text{ and }\,\, X_n \cap \bigcup_{\substack{k \in \omega: \\ M_k \cap \,\bigcup_{i\le n-1}X_i \neq \emptyset}} M_k =\emptyset, \end{align} $$
$$ \begin{align} \forall n \in \omega,\quad \varphi_n(F_n) \ge \frac{\inf_{k \in \omega}\| \omega\|_{\varphi_k}}{2} \,\,\text{ and }\,\, X_n \cap \bigcup_{\substack{k \in \omega: \\ M_k \cap \,\bigcup_{i\le n-1}X_i \neq \emptyset}} M_k =\emptyset, \end{align} $$
where
![]() $X_n:=\{n\} \times F_n$
for each n.
$X_n:=\{n\} \times F_n$
for each n.
Set
![]() $X:=\bigcup _n X_n$
. Then
$X:=\bigcup _n X_n$
. Then
![]() $X\notin \mathrm {Exh}(\psi )$
. Indeed
$X\notin \mathrm {Exh}(\psi )$
. Indeed
 $$ \begin{align*} \begin{split} \|X\|_\psi &=\inf_{F \in \mathrm{Fin}}\sup_{n \in \omega}(\sum_{k \in S_n} a_k \varphi_k^{q_n}(X_{(k)}\setminus F))^{1/q_n}\\ &\ge \inf_{F \in \mathrm{Fin}}\sup_{n \in \omega} \min_{k \in S_n}\{\varphi_k(X_{(k)}\setminus F)\} \ge \frac{\inf_{k \in \omega}\| \omega\|_{\varphi_k}}{2}>0. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \|X\|_\psi &=\inf_{F \in \mathrm{Fin}}\sup_{n \in \omega}(\sum_{k \in S_n} a_k \varphi_k^{q_n}(X_{(k)}\setminus F))^{1/q_n}\\ &\ge \inf_{F \in \mathrm{Fin}}\sup_{n \in \omega} \min_{k \in S_n}\{\varphi_k(X_{(k)}\setminus F)\} \ge \frac{\inf_{k \in \omega}\| \omega\|_{\varphi_k}}{2}>0. \end{split} \end{align*} $$
It follows that
![]() $X \notin \mathrm {Exh}(\sup _n \mu _n)$
, i.e., there exist
$X \notin \mathrm {Exh}(\sup _n \mu _n)$
, i.e., there exist
![]() $\varepsilon>0$
and an increasing sequence
$\varepsilon>0$
and an increasing sequence
![]() $(n_k)$
in
$(n_k)$
in
![]() $\omega $
such that
$\omega $
such that
![]() $\mu _{n_k}(X)>\varepsilon $
for all
$\mu _{n_k}(X)>\varepsilon $
for all
![]() $k \in \omega $
. However, thanks to (9), for each k there exists a unique
$k \in \omega $
. However, thanks to (9), for each k there exists a unique
![]() $m_k \in \omega $
such that
$m_k \in \omega $
such that
![]() $X\cap M_{n_k}\subseteq X_{m_k}$
. Therefore
$X\cap M_{n_k}\subseteq X_{m_k}$
. Therefore
![]() $\mu _{n_k}(X_{m_k})>\varepsilon $
for all
$\mu _{n_k}(X_{m_k})>\varepsilon $
for all
![]() $k \in \omega $
. Let M be an infinite subset of
$k \in \omega $
. Let M be an infinite subset of
![]() $\{m_k: k \in \omega \}$
such that
$\{m_k: k \in \omega \}$
such that
![]() $|S_n \cap M|\le 1$
for all n. Define
$|S_n \cap M|\le 1$
for all n. Define
![]() $Y:=\bigcup _{m \in M}X_m$
and note that
$Y:=\bigcup _{m \in M}X_m$
and note that
![]() $Y\notin \mathrm {Exh}(\sup _n \mu _n)$
.
$Y\notin \mathrm {Exh}(\sup _n \mu _n)$
.
Then necessarily
![]() $Y\notin \mathrm {Exh}(\psi )$
. However, considering that there is at most one
$Y\notin \mathrm {Exh}(\psi )$
. However, considering that there is at most one
![]() $k \in S_n$
such that
$k \in S_n$
such that
![]() $Y_{(k)}\neq \emptyset $
, we obtain
$Y_{(k)}\neq \emptyset $
, we obtain
 $$ \begin{align*} \|Y\|_\psi &\le \inf_{F \in [\omega^2]^{<\omega}}\sup_{n \in \omega} \max_{k \in S_n}\{a_k^{1/q_n}\varphi_k((Y\setminus F)_{(k)})\} \\ & \le \sup_{n \in \omega}\varphi_n(\omega) \limsup_{t\to \infty}\max_{k \in S_t}\{a_k^{1/q_t}\} = 0, \end{align*} $$
$$ \begin{align*} \|Y\|_\psi &\le \inf_{F \in [\omega^2]^{<\omega}}\sup_{n \in \omega} \max_{k \in S_n}\{a_k^{1/q_n}\varphi_k((Y\setminus F)_{(k)})\} \\ & \le \sup_{n \in \omega}\varphi_n(\omega) \limsup_{t\to \infty}\max_{k \in S_t}\{a_k^{1/q_t}\} = 0, \end{align*} $$
which is the wanted contradiction.⊣
With the same technique of Corollary 4.17, we obtain (details are omitted):
Corollary 4.19. Let
![]() $\varphi $
be a strongly-density-like lscsm on
$\varphi $
be a strongly-density-like lscsm on
![]() $\omega $
such that
$\omega $
such that
Moreover, let
![]() $\psi =\psi (\boldsymbol {\varphi },q,a,S)$
be a lscsm on
$\psi =\psi (\boldsymbol {\varphi },q,a,S)$
be a lscsm on
![]() $\omega ^2$
as in (7) and assume that
$\omega ^2$
as in (7) and assume that
![]() $\boldsymbol {\varphi }$
is the constant sequence
$\boldsymbol {\varphi }$
is the constant sequence
![]() $(\varphi )$
, q is a bounded sequence, and
$(\varphi )$
, q is a bounded sequence, and
![]() $\lim _n a_n=0$
. Then
$\lim _n a_n=0$
. Then
![]() $\mathrm {Exh}(\psi )$
is not a generalized density ideal.
$\mathrm {Exh}(\psi )$
is not a generalized density ideal.
Note that condition (10) has been already used in the literature, see e.g., [Reference Solecki22, Theorem 3.1].
Putting all together, we have the following:
Theorem 4.20. Let
![]() $\psi =\psi (\boldsymbol {\varphi }, q, a, S)$
be a lscsm on
$\psi =\psi (\boldsymbol {\varphi }, q, a, S)$
be a lscsm on
![]() $\omega ^2$
as in (7) such that:
$\omega ^2$
as in (7) such that:
-
(i)
 $\mathrm {Exh}(\varphi _n)$
is tall for each
$\mathrm {Exh}(\varphi _n)$
is tall for each
 $n \in \omega $
;
$n \in \omega $
; -
(ii)
 $\lim _n \max \{a_k^{1/q_n}: k \in S_n\}=0$
;
$\lim _n \max \{a_k^{1/q_n}: k \in S_n\}=0$
; -
(iii)
 $\inf _n c(\varphi _n)>0$
; and
$\inf _n c(\varphi _n)>0$
; and -
(iv)
 $0<\inf _{n}\| \omega \|_{\varphi _n} \le \sup _{n} \varphi _n(\omega ) <\infty $
.
$0<\inf _{n}\| \omega \|_{\varphi _n} \le \sup _{n} \varphi _n(\omega ) <\infty $
.
Then
![]() $\mathrm {Exh}(\psi )$
is a tall density-like ideal which is not a generalized density ideal.
$\mathrm {Exh}(\psi )$
is a tall density-like ideal which is not a generalized density ideal.
Proof. Thanks to (iv), we have
![]() $\sup _{n,k}\varphi _n(\{k\})\le \sup _n \varphi _n(\omega )<\infty $
. The conclusion follows by Proposition 4.16 and Theorems 4.13 and 4.18.⊣
$\sup _{n,k}\varphi _n(\{k\})\le \sup _n \varphi _n(\omega )<\infty $
. The conclusion follows by Proposition 4.16 and Theorems 4.13 and 4.18.⊣
In the case where
![]() $\boldsymbol {\varphi }$
is a constant sequence and q is bounded, we can simplify the above conditions:
$\boldsymbol {\varphi }$
is a constant sequence and q is bounded, we can simplify the above conditions:
Corollary 4.21. Let
![]() $\varphi $
be a strongly-density-like lscsm on
$\varphi $
be a strongly-density-like lscsm on
![]() $\omega $
such that
$\omega $
such that
![]() $\mathrm {Exh}(\varphi )$
is tall and satisfies (10). Moreover, let
$\mathrm {Exh}(\varphi )$
is tall and satisfies (10). Moreover, let
![]() $\psi =\psi (\boldsymbol {\varphi }, q, a, S)$
be a lscsm on
$\psi =\psi (\boldsymbol {\varphi }, q, a, S)$
be a lscsm on
![]() $\omega ^2$
as in (7) such that
$\omega ^2$
as in (7) such that
![]() $\boldsymbol {\varphi }$
is the constant sequence
$\boldsymbol {\varphi }$
is the constant sequence
![]() $(\varphi )$
, q is bounded, and
$(\varphi )$
, q is bounded, and
![]() $\lim _n a_n=0$
.
$\lim _n a_n=0$
.
Then
![]() $\mathrm {Exh}(\psi )$
is a tall density-like ideal which is not a generalized density ideal.
$\mathrm {Exh}(\psi )$
is a tall density-like ideal which is not a generalized density ideal.
Thus, we answer Question 3, giving an alternative proof of Theorem 1.3.
Theorem 4.22. There exists a tall density-like ideal which is not a generalized density ideal.
Proof. Let
![]() $\mathcal {I}_d$
be the ideal of density zero sets, which is a tall ideal. Thanks to [Reference Farah6, Example 1.2.3(d), Theorem 1.13.3(a), and Lemma 1.13.9(Z3)], there exists a sequence
$\mathcal {I}_d$
be the ideal of density zero sets, which is a tall ideal. Thanks to [Reference Farah6, Example 1.2.3(d), Theorem 1.13.3(a), and Lemma 1.13.9(Z3)], there exists a sequence
![]() $(\mu _n)$
of probability measures with finite pairwise disjoint supports such that
$(\mu _n)$
of probability measures with finite pairwise disjoint supports such that
![]() $\mathcal {I}_d=\mathrm {Exh}(\varphi )$
, where
$\mathcal {I}_d=\mathrm {Exh}(\varphi )$
, where
![]() $\varphi :=\sup _n \mu _n$
. In particular,
$\varphi :=\sup _n \mu _n$
. In particular,
![]() $\varphi (\omega )=\|\omega \|_\varphi =1$
. The claim follows by Corollary 4.21.⊣
$\varphi (\omega )=\|\omega \|_\varphi =1$
. The claim follows by Corollary 4.21.⊣
With the same spirit of Question 2, we ask:
Question 4. How many pairwise nonisomorphic tall density-like ideals which are not generalized density ideals are there?
We will show that, as in Theorem 3.7, there is a family of
![]() $2^\omega $
such ideals. To this aim, we need a preliminary lemma.
$2^\omega $
such ideals. To this aim, we need a preliminary lemma.
Lemma 4.23. There exists a family
![]() $\mathscr {A}$
of
$\mathscr {A}$
of
![]() $2^\omega $
subsets of
$2^\omega $
subsets of
![]() $\omega ^2$
such that
$\omega ^2$
such that
 $$ \begin{align} \forall (A,A^\prime) \in [\mathscr{A}]^2, \forall k \in \omega,\quad A_{(k)} \notin \mathrm{Fin} \,\,\,\text{ and }\,\,\, A \cap A^\prime \in \mathrm{Fin}. \end{align} $$
$$ \begin{align} \forall (A,A^\prime) \in [\mathscr{A}]^2, \forall k \in \omega,\quad A_{(k)} \notin \mathrm{Fin} \,\,\,\text{ and }\,\,\, A \cap A^\prime \in \mathrm{Fin}. \end{align} $$
Proof. It is known that there exists a family
![]() $\mathscr {B}$
of
$\mathscr {B}$
of
![]() $2^\omega $
subsets of
$2^\omega $
subsets of
![]() $\omega $
such that
$\omega $
such that
 $$ \begin{align*}\forall (B,B^\prime) \in [\mathscr{B}]^2, \quad B \notin \mathrm{Fin} \,\,\,\text{ and }\,\,\, B \cap B^\prime \in \mathrm{Fin}, \end{align*} $$
$$ \begin{align*}\forall (B,B^\prime) \in [\mathscr{B}]^2, \quad B \notin \mathrm{Fin} \,\,\,\text{ and }\,\,\, B \cap B^\prime \in \mathrm{Fin}, \end{align*} $$
see e.g., [Reference Albiac and Kalton1, Lemma 2.5.3]. Then, it is sufficient to see that
 $\{\,\bigcup _{n\in \omega } \{n\}\times (B\setminus n): B \in \mathscr {B}\}$
satisfies (11).⊣
$\{\,\bigcup _{n\in \omega } \{n\}\times (B\setminus n): B \in \mathscr {B}\}$
satisfies (11).⊣
Theorem 4.24. There are
![]() $2^\omega $
nonpathological and pairwise nonisomorphic tall density-like ideals which are not generalized density ideals.
$2^\omega $
nonpathological and pairwise nonisomorphic tall density-like ideals which are not generalized density ideals.
Proof. Let
![]() $h: \omega ^2 \to \omega $
be the bijection defined in (1). Let also
$h: \omega ^2 \to \omega $
be the bijection defined in (1). Let also
![]() $\mathscr {M}=\{M_z: z \in \omega ^2\}$
be a partition of
$\mathscr {M}=\{M_z: z \in \omega ^2\}$
be a partition of
![]() $\omega ^2$
into nonempty finite sets such that
$\omega ^2$
into nonempty finite sets such that
![]() $M_{(n,m)}\subseteq \{n\}\times \omega $
for all
$M_{(n,m)}\subseteq \{n\}\times \omega $
for all
![]() $n,m\in \omega $
and
$n,m\in \omega $
and
 $$ \begin{align} \forall n \in \omega, \quad m_{h^{-1}(n+1)}\ge (n+2)\sum_{i\le n}m_{h^{-1}(i)}, \end{align} $$
$$ \begin{align} \forall n \in \omega, \quad m_{h^{-1}(n+1)}\ge (n+2)\sum_{i\le n}m_{h^{-1}(i)}, \end{align} $$
where
![]() $m_z:=|M_z|$
. Moreover, for each
$m_z:=|M_z|$
. Moreover, for each
![]() $(n,m) \in \omega ^2$
, let
$(n,m) \in \omega ^2$
, let
![]() $\mu _{(n,m)}$
be the uniform probability measure given by
$\mu _{(n,m)}$
be the uniform probability measure given by
![]() $\mu _{(n,m)}(X)= |(\{n\}\times X)\cap M_{(n,m)}|/m_{(n,m)}$
for all
$\mu _{(n,m)}(X)= |(\{n\}\times X)\cap M_{(n,m)}|/m_{(n,m)}$
for all
![]() $X\subseteq \omega $
.
$X\subseteq \omega $
.
Fix
![]() $(S_n) \in \mathcal {F}_{\mathrm {incr}}$
such that
$(S_n) \in \mathcal {F}_{\mathrm {incr}}$
such that
![]() $\lim _n |S_n|=\infty $
and let
$\lim _n |S_n|=\infty $
and let
![]() $\mathscr {A}$
be a family of
$\mathscr {A}$
be a family of
![]() $2^\omega $
subsets of
$2^\omega $
subsets of
![]() $\omega ^2$
which satisfies (11) (existing by Lemma 4.23). For each
$\omega ^2$
which satisfies (11) (existing by Lemma 4.23). For each
![]() $A \in \mathscr {A}$
, let
$A \in \mathscr {A}$
, let
![]() $\psi _A$
be the lscsm on
$\psi _A$
be the lscsm on
![]() $\omega ^2$
defined by
$\omega ^2$
defined by
 $$ \begin{align*} \psi_A:=\sup_{n\in \omega} \sum_{k \in S_n}\frac{1}{|S_n|}\,\varphi_{A,k}, \,\,\,\text{ where }\,\,\,\varphi_{A,k}:=\sup_{t \in A_{(k)}} \mu_{(k,t)}, \end{align*} $$
$$ \begin{align*} \psi_A:=\sup_{n\in \omega} \sum_{k \in S_n}\frac{1}{|S_n|}\,\varphi_{A,k}, \,\,\,\text{ where }\,\,\,\varphi_{A,k}:=\sup_{t \in A_{(k)}} \mu_{(k,t)}, \end{align*} $$
for all
![]() $k \in \omega $
. It follows that, for each
$k \in \omega $
. It follows that, for each
![]() $A \in \mathscr {A}$
, the lscsm
$A \in \mathscr {A}$
, the lscsm
![]() $\psi _A$
is of the type (7), where
$\psi _A$
is of the type (7), where
![]() $q_n=1$
for all n and
$q_n=1$
for all n and
![]() $a_k=1/|S_i|$
whenever
$a_k=1/|S_i|$
whenever
![]() $k \in S_i$
; hence
$k \in S_i$
; hence
![]() $\lim _n a_n=0$
. In addition, for each
$\lim _n a_n=0$
. In addition, for each
![]() $A \in \mathscr {A}$
and
$A \in \mathscr {A}$
and
![]() $k \in \omega $
, the ideal
$k \in \omega $
, the ideal
![]() $\mathrm {Exh}(\varphi _{A,k})$
is tall and
$\mathrm {Exh}(\varphi _{A,k})$
is tall and
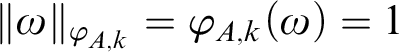 $\|\omega \|_{\varphi _{A,k}}=\varphi _{A,k}(\omega )=1$
. Lastly, thanks to Remark 4.5, each
$\|\omega \|_{\varphi _{A,k}}=\varphi _{A,k}(\omega )=1$
. Lastly, thanks to Remark 4.5, each
![]() $\varphi _{A,k}$
is strongly-density-like with any witnessing constant
$\varphi _{A,k}$
is strongly-density-like with any witnessing constant
![]() $c(\varphi _{A,k})<1$
. In particular,
$c(\varphi _{A,k})<1$
. In particular,
![]() . Therefore, by Theorem 4.20, each
. Therefore, by Theorem 4.20, each
![]() $\mathrm {Exh}(\psi _A)$
is a tall density-like ideal which is not a generalized density ideal. Also, by Remark 4.10, each
$\mathrm {Exh}(\psi _A)$
is a tall density-like ideal which is not a generalized density ideal. Also, by Remark 4.10, each
![]() $\mathrm {Exh}(\psi _A)$
is nonpathological.
$\mathrm {Exh}(\psi _A)$
is nonpathological.
At this point, we claim that, for all distinct
![]() $A,A^\prime \in \mathscr {A}$
, the ideals
$A,A^\prime \in \mathscr {A}$
, the ideals
![]() $\mathrm {Exh}(\psi _A)$
and
$\mathrm {Exh}(\psi _A)$
and
![]() $\mathrm {Exh}(\psi _{A^\prime })$
are not isomorphic. To this aim, fix distinct
$\mathrm {Exh}(\psi _{A^\prime })$
are not isomorphic. To this aim, fix distinct
![]() $A,A^\prime \in \mathscr {A}$
and suppose for the sake of contradiction that
$A,A^\prime \in \mathscr {A}$
and suppose for the sake of contradiction that
![]() $\mathrm {Exh}(\psi _A)$
and
$\mathrm {Exh}(\psi _A)$
and
![]() $\mathrm {Exh}(\psi _{A^\prime })$
are isomorphic, witnessed by a bijection
$\mathrm {Exh}(\psi _{A^\prime })$
are isomorphic, witnessed by a bijection
![]() $f:\omega ^2 \to \omega ^2$
. Let
$f:\omega ^2 \to \omega ^2$
. Let
![]() $(x_n)$
be the enumeration of the infinite set
$(x_n)$
be the enumeration of the infinite set
![]() $A\setminus A^\prime $
such that the sequence
$A\setminus A^\prime $
such that the sequence
![]() $(h(x_n))$
is increasing. Then, pick a sequence
$(h(x_n))$
is increasing. Then, pick a sequence
![]() $(F_n) \in \mathcal {F}_{\mathrm {disj}}$
such that
$(F_n) \in \mathcal {F}_{\mathrm {disj}}$
such that
 $$ \begin{align*}\forall n \in \omega,\quad F_n\subseteq M_{x_n}, \,\,\, |F_n|=\left\lfloor \frac{m_{x_n}}{2}\right\rfloor, \,\,\,\text{ and }\,\,\, F_{n+1}\cap \bigcup_{\substack{z \in \omega^2: \\ h(z)<h(x_{n+1})}}f[M_z]=\emptyset. \end{align*} $$
$$ \begin{align*}\forall n \in \omega,\quad F_n\subseteq M_{x_n}, \,\,\, |F_n|=\left\lfloor \frac{m_{x_n}}{2}\right\rfloor, \,\,\,\text{ and }\,\,\, F_{n+1}\cap \bigcup_{\substack{z \in \omega^2: \\ h(z)<h(x_{n+1})}}f[M_z]=\emptyset. \end{align*} $$
Note that this is really possible: indeed, letting U be the latter union, it follows by (12) that
 $$ \begin{align*} |U|= \sum_{h(z)<h(x_{n+1})}m_z= \sum_{i\le h(x_{n+1})-1}m_{h^{-1}(i)} \le \frac{1}{2}\,m_{x_{n+1}}. \end{align*} $$
$$ \begin{align*} |U|= \sum_{h(z)<h(x_{n+1})}m_z= \sum_{i\le h(x_{n+1})-1}m_{h^{-1}(i)} \le \frac{1}{2}\,m_{x_{n+1}}. \end{align*} $$
Set
![]() $F:=\bigcup _n F_n$
. It follows by construction that
$F:=\bigcup _n F_n$
. It follows by construction that
![]() for all
for all
![]() $k \in \omega $
, hence
$k \in \omega $
, hence
![]() $F \notin \mathrm {Exh}(\psi _A)$
. On the other hand, we obtain by (12) that
$F \notin \mathrm {Exh}(\psi _A)$
. On the other hand, we obtain by (12) that
 $$ \begin{align*} \begin{split} \forall (i,j) \in A^\prime \setminus A,\quad \mu_{(i,j)}((f^{-1}[F])_{(i)}) &=\frac{|F\cap f[M_{(i,j)}]|}{m_{(i,j)}} \\ &\le \frac{\sum_{n\in\{k:\ h(x_k)<h((i,j))\}}|F_n|}{m_{(i,j)}} \\ &\le \frac{\sum_{k\le h((i,j))-1}m_{h^{-1}(k)}}{m_{h^{-1}(h((i,j)))}} \le \frac{1}{h((i,j))+1}, \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \forall (i,j) \in A^\prime \setminus A,\quad \mu_{(i,j)}((f^{-1}[F])_{(i)}) &=\frac{|F\cap f[M_{(i,j)}]|}{m_{(i,j)}} \\ &\le \frac{\sum_{n\in\{k:\ h(x_k)<h((i,j))\}}|F_n|}{m_{(i,j)}} \\ &\le \frac{\sum_{k\le h((i,j))-1}m_{h^{-1}(k)}}{m_{h^{-1}(h((i,j)))}} \le \frac{1}{h((i,j))+1}, \end{split} \end{align*} $$
which implies that
![]() $f^{-1}[F] \in \mathrm {Exh}(\psi _{A^\prime })$
. This contradiction concludes the proof.⊣
$f^{-1}[F] \in \mathrm {Exh}(\psi _{A^\prime })$
. This contradiction concludes the proof.⊣
5 Characterization of generalized density ideals
In this section, we provide a characterization of generalized density ideals which resembles the one of density-like ideal given in Definition 1.2. This provides sufficient conditions for a density-like ideal to be necessarily a generalized density ideal,
Let
![]() $\mathscr {H}$
be the set of strictly increasing sequences in
$\mathscr {H}$
be the set of strictly increasing sequences in
![]() $\omega $
. Then, given a lscsm
$\omega $
. Then, given a lscsm
![]() $\varphi $
and a real
$\varphi $
and a real
![]() $\varepsilon>0$
, define
$\varepsilon>0$
, define
for all
![]() $s=(s_n) \in \mathscr {H}$
and
$s=(s_n) \in \mathscr {H}$
and
![]() $F=(F_n) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi , \varepsilon }$
(note that
$F=(F_n) \in \mathcal {F}_{\mathrm {disj}} \cap \mathcal {G}_{\varphi , \varepsilon }$
(note that
![]() $K_{s, F}\neq \emptyset $
).
$K_{s, F}\neq \emptyset $
).
Definition 5.1. A lscsm
![]() $\varphi $
on
$\varphi $
on
![]() $\omega $
satisfies condition
$\omega $
satisfies condition
![]() $\boldsymbol {\mathrm {D}_{\mathrm {weak}}}$
if for all
$\boldsymbol {\mathrm {D}_{\mathrm {weak}}}$
if for all
![]() $\varepsilon>0$
there exist
$\varepsilon>0$
there exist
![]() $\delta>0$
and a sequence
$\delta>0$
and a sequence
![]() $s \in \mathscr {H}$
such that, if
$s \in \mathscr {H}$
such that, if
![]() $F=(F_n) \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\varphi ,\delta }$
and
$F=(F_n) \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\varphi ,\delta }$
and
![]() $k\in K_{s, F}$
, then
$k\in K_{s, F}$
, then
![]() $\varphi (\bigcup _{n} F_{k_n})<\varepsilon $
.
$\varphi (\bigcup _{n} F_{k_n})<\varepsilon $
.
If the sequence
![]() $s \in \mathscr {H}$
can be chosen uniformly in
$s \in \mathscr {H}$
can be chosen uniformly in
![]() $\varepsilon>0$
, we have the following:
$\varepsilon>0$
, we have the following:
Definition 5.2. A lscsm
![]() $\varphi $
on
$\varphi $
on
![]() $\omega $
satisfies condition
$\omega $
satisfies condition
![]() $\boldsymbol {\mathrm {D}_{\mathrm {strong}}}$
if there exists a sequence
$\boldsymbol {\mathrm {D}_{\mathrm {strong}}}$
if there exists a sequence
![]() $s \in \mathscr {H}$
for which for all
$s \in \mathscr {H}$
for which for all
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $\delta>0$
such that, if
$\delta>0$
such that, if
![]() $F=(F_n) \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\varphi ,\delta }$
and
$F=(F_n) \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\varphi ,\delta }$
and
![]() $k\in K_{s, F}$
, then
$k\in K_{s, F}$
, then
![]() $\varphi (\bigcup _{n} F_{k_n})<\varepsilon $
.
$\varphi (\bigcup _{n} F_{k_n})<\varepsilon $
.
It is clear that every lscsm
![]() $\varphi $
satisfying condition
$\varphi $
satisfying condition
![]() $\mathrm {D}_{\mathrm {strong}}$
satisfies also condition
$\mathrm {D}_{\mathrm {strong}}$
satisfies also condition
![]() $\mathrm {D}_{\mathrm {weak}}$
. Thus, we state the main result of this section.
$\mathrm {D}_{\mathrm {weak}}$
. Thus, we state the main result of this section.
Theorem 5.3. Let
![]() $\mathcal {I}$
be an ideal. Then the following are equivalent:
$\mathcal {I}$
be an ideal. Then the following are equivalent:
-
(A1)
 $\mathcal {I}$
is a generalized density ideal;
$\mathcal {I}$
is a generalized density ideal; -
(A2) every lscsm
 $\varphi $
such that
$\varphi $
such that
 $\mathcal {I}=\mathrm {Exh}(\varphi )$
satisfies condition
$\mathcal {I}=\mathrm {Exh}(\varphi )$
satisfies condition
 $\mathrm {D}_{\mathrm {strong}}$
;
$\mathrm {D}_{\mathrm {strong}}$
; -
(A3) every lscsm
 $\varphi $
such that
$\varphi $
such that
 $\mathcal {I}=\mathrm {Exh}(\varphi )$
satisfies condition
$\mathcal {I}=\mathrm {Exh}(\varphi )$
satisfies condition
 $\mathrm {D}_{\mathrm {weak}}$
;
$\mathrm {D}_{\mathrm {weak}}$
; -
(A4)
 $\mathcal {I}=\mathrm {Exh}(\varphi )$
for some lscsm
$\mathcal {I}=\mathrm {Exh}(\varphi )$
for some lscsm
 $\varphi $
satisfying condition
$\varphi $
satisfying condition
 $\mathrm {D}_{\mathrm {strong}}$
; and
$\mathrm {D}_{\mathrm {strong}}$
; and -
(A5)
 $\mathcal {I}=\mathrm {Exh}(\varphi )$
for some lscsm
$\mathcal {I}=\mathrm {Exh}(\varphi )$
for some lscsm
 $\varphi $
satisfying condition
$\varphi $
satisfying condition
 $\mathrm {D}_{\mathrm {weak}}$
.
$\mathrm {D}_{\mathrm {weak}}$
.
The proof is divided in some intermediate steps.
Lemma 5.4. Let
![]() $\varphi $
be a lscsm and assume that
$\varphi $
be a lscsm and assume that
![]() $\mathrm {Exh}(\varphi )$
is a generalized density ideal. Then
$\mathrm {Exh}(\varphi )$
is a generalized density ideal. Then
![]() $\varphi $
satisfies condition
$\varphi $
satisfies condition
![]() $\mathrm {D}_{\mathrm {strong}}$
.
$\mathrm {D}_{\mathrm {strong}}$
.
Proof. Let us suppose for the sake of contradiction that
![]() $\varphi $
does not satisfy condition
$\varphi $
does not satisfy condition
![]() $\mathrm {D}_{\mathrm {strong}}$
. Thanks to Proposition 2.1, we can suppose without loss of generality that there exist a sequence
$\mathrm {D}_{\mathrm {strong}}$
. Thanks to Proposition 2.1, we can suppose without loss of generality that there exist a sequence
![]() $(\mu _n)$
of submeasures and a sequence
$(\mu _n)$
of submeasures and a sequence
![]() $(S_n) \in \mathcal {F}_{\mathrm {int}}$
of consecutive intervals of
$(S_n) \in \mathcal {F}_{\mathrm {int}}$
of consecutive intervals of
![]() $\omega $
such that
$\omega $
such that
![]() $\varphi =\sup _n\mu _n$
and
$\varphi =\sup _n\mu _n$
and
![]() $S_n=\mathrm {supp}(\mu _n)$
for all
$S_n=\mathrm {supp}(\mu _n)$
for all
![]() $n \in \omega $
. In particular,
$n \in \omega $
. In particular,
![]() $\mathrm {Exh}(\varphi )=\{A\subseteq \omega : \lim _n \mu _n(A)=0\}$
and
$\mathrm {Exh}(\varphi )=\{A\subseteq \omega : \lim _n \mu _n(A)=0\}$
and
![]() $\mu _n(\omega )\not \to 0$
.
$\mu _n(\omega )\not \to 0$
.
Define
![]() $s \in \mathscr {H}$
by
$s \in \mathscr {H}$
by
![]() $s_n:=\max S_n$
for all
$s_n:=\max S_n$
for all
![]() $n \in \omega $
. Since
$n \in \omega $
. Since
![]() $\varphi $
does not satisfy condition
$\varphi $
does not satisfy condition
![]() $\mathrm {D}_{\mathrm {strong}}$
, there exists
$\mathrm {D}_{\mathrm {strong}}$
, there exists
![]() $\varepsilon>0$
such that for all nonzero
$\varepsilon>0$
such that for all nonzero
![]() $m\in \omega $
there are
$m\in \omega $
there are
 $F^m=(F^m_n)\in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\varphi ,\frac {\varepsilon }{2^m}}$
and
$F^m=(F^m_n)\in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\varphi ,\frac {\varepsilon }{2^m}}$
and
![]() $k^m=(k^m_n)\in K_{s,F^m}$
for which
$k^m=(k^m_n)\in K_{s,F^m}$
for which
 $\varphi (\bigcup _{n} F^m_{k_n^m})\geq \varepsilon $
. Since
$\varphi (\bigcup _{n} F^m_{k_n^m})\geq \varepsilon $
. Since
![]() $\varphi $
is a lscsm, for each m there exists
$\varphi $
is a lscsm, for each m there exists
![]() $\ell _m \in \omega $
such that
$\ell _m \in \omega $
such that
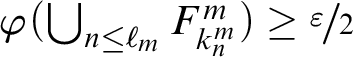 .
.
Set
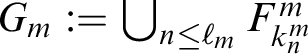 $G_m:=\bigcup _{n\leq \ell _m} F^m_{k^m_n}$
and note that
$G_m:=\bigcup _{n\leq \ell _m} F^m_{k^m_n}$
and note that
![]() $G:=\bigcup _m G_m$
does not belong to
$G:=\bigcup _m G_m$
does not belong to
![]() $\mathrm {Exh}(\varphi )$
. To this aim, fix a nonzero
$\mathrm {Exh}(\varphi )$
. To this aim, fix a nonzero
![]() $j\in \omega $
. Since
$j\in \omega $
. Since
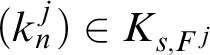 $(k^j_n)\in K_{s,F^j}$
, there are at most j many sets
$(k^j_n)\in K_{s,F^j}$
, there are at most j many sets
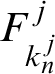 $F^j_{k_n^j}$
which have nonempty intersection with the set
$F^j_{k_n^j}$
which have nonempty intersection with the set
![]() $s_j+1$
and each of them has
$s_j+1$
and each of them has
![]() $\varphi $
-value smaller than
$\varphi $
-value smaller than
![]() $\varepsilon /2^{j}$
. Thus
$\varepsilon /2^{j}$
. Thus
 $$ \begin{align*} \begin{split} \varphi(G\setminus (s_j+1)) \ge \varphi(G_j\setminus (s_j+1))\ge \varphi(G_j)-\varphi(G_j \cap (s_j+1))\ge \varepsilon-j \frac{\varepsilon}{2^j}\ge \frac{\varepsilon}{2}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \varphi(G\setminus (s_j+1)) \ge \varphi(G_j\setminus (s_j+1))\ge \varphi(G_j)-\varphi(G_j \cap (s_j+1))\ge \varepsilon-j \frac{\varepsilon}{2^j}\ge \frac{\varepsilon}{2}. \end{split} \end{align*} $$
Therefore
![]() . In particular, there exists a sequence
. In particular, there exists a sequence
![]() $(j_i) \in \mathscr {H}$
such that
$(j_i) \in \mathscr {H}$
such that
![]() for all
for all
![]() $i\in \omega $
. Passing eventually to a subsequence, we can assume without loss of generality that
$i\in \omega $
. Passing eventually to a subsequence, we can assume without loss of generality that
At this point, define
![]() $X:=G\cap \bigcup _i S_{j_i}$
. Then by construction
$X:=G\cap \bigcup _i S_{j_i}$
. Then by construction
![]() , so that
, so that
![]() $X\notin \mathrm {Exh}(\varphi )$
. On the other hand, we will show that
$X\notin \mathrm {Exh}(\varphi )$
. On the other hand, we will show that
![]() $\lim _n \mu _n(X)=0$
, reaching a contradiction. Taking into account (13), note that
$\lim _n \mu _n(X)=0$
, reaching a contradiction. Taking into account (13), note that
![]() $S_{j_i}\cap X= S_{j_i} \cap \bigcup _{m>i}G_m$
for all i. Moreover, recall that, for all
$S_{j_i}\cap X= S_{j_i} \cap \bigcup _{m>i}G_m$
for all i. Moreover, recall that, for all
![]() $i,m \in \omega $
, there exists at most one n such that
$i,m \in \omega $
, there exists at most one n such that
 $F^m_{k^m_n}\cap S_{j_i} \neq \emptyset $
. It follows that
$F^m_{k^m_n}\cap S_{j_i} \neq \emptyset $
. It follows that
 $$ \begin{align*}\forall i \in \omega,\quad \varphi(S_{j_i}\cap X)=\mu_{j_i}\left(\bigcup_{m>i}G_m\right)\le \sum_{m>i}\mu_{j_i}(G_m) \le \sum_{m>i}\frac{\varepsilon}{2^m}=\frac{\varepsilon}{2^i}. \end{align*} $$
$$ \begin{align*}\forall i \in \omega,\quad \varphi(S_{j_i}\cap X)=\mu_{j_i}\left(\bigcup_{m>i}G_m\right)\le \sum_{m>i}\mu_{j_i}(G_m) \le \sum_{m>i}\frac{\varepsilon}{2^m}=\frac{\varepsilon}{2^i}. \end{align*} $$
To conclude, we obtain that
 $$ \begin{align*}\forall t \in \omega, \quad \varphi\left(X\setminus \bigcup_{i\le t}S_{j_i}\right)=\varphi\left(X\cap \bigcup_{i> t}S_{j_i}\right)\le \sum_{i>t}\varphi(S_{j_i} \cap X)\le \sum_{i>t}\frac{\varepsilon}{2^i}= \frac{\varepsilon}{2^t}, \end{align*} $$
$$ \begin{align*}\forall t \in \omega, \quad \varphi\left(X\setminus \bigcup_{i\le t}S_{j_i}\right)=\varphi\left(X\cap \bigcup_{i> t}S_{j_i}\right)\le \sum_{i>t}\varphi(S_{j_i} \cap X)\le \sum_{i>t}\frac{\varepsilon}{2^i}= \frac{\varepsilon}{2^t}, \end{align*} $$
which tends to
![]() $0$
as
$0$
as
![]() $t\to \infty $
. Hence
$t\to \infty $
. Hence
![]() $X \in \mathrm {Exh}(\varphi )$
, which is the wanted contradiction.⊣
$X \in \mathrm {Exh}(\varphi )$
, which is the wanted contradiction.⊣
Now, we show that condition
![]() $\mathrm {D}_{\mathrm {weak}}$
implies (a variant of) condition
$\mathrm {D}_{\mathrm {weak}}$
implies (a variant of) condition
![]() $\mathrm {D}_{\mathrm {strong}}$
.
$\mathrm {D}_{\mathrm {strong}}$
.
Lemma 5.5. Let
![]() $\varphi $
be a lscsm which satisfies condition
$\varphi $
be a lscsm which satisfies condition
![]() $\mathrm {D}_{\mathrm {weak}}$
. Then there is a lscsm
$\mathrm {D}_{\mathrm {weak}}$
. Then there is a lscsm
![]() $\nu $
and a sequence
$\nu $
and a sequence
![]() $s \in \mathscr {H}$
such that for every
$s \in \mathscr {H}$
such that for every
![]() $\varepsilon>0$
there is
$\varepsilon>0$
there is
![]() $\delta>0$
for which, if
$\delta>0$
for which, if
![]() $F \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\nu ,\delta }$
and
$F \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\nu ,\delta }$
and
![]() $k \in K_{s,F}$
, then
$k \in K_{s,F}$
, then
![]() $\nu (\bigcup _{n} F_{k_{2n}})<\varepsilon $
, and
$\nu (\bigcup _{n} F_{k_{2n}})<\varepsilon $
, and
![]() $\mathrm {Exh}(\varphi )=\mathrm {Exh}(\nu )$
.
$\mathrm {Exh}(\varphi )=\mathrm {Exh}(\nu )$
.
Proof. Let
![]() $(\varepsilon _k)$
be a strictly decreasing sequence such that
$(\varepsilon _k)$
be a strictly decreasing sequence such that
![]() $\lim _k \varepsilon _k=0$
. Then, for each k, there are
$\lim _k \varepsilon _k=0$
. Then, for each k, there are
![]() $\delta _k>0$
and a sequence
$\delta _k>0$
and a sequence
![]() $s^k=(s_n^k) \in \mathscr {H}$
such that, if
$s^k=(s_n^k) \in \mathscr {H}$
such that, if
![]() $F \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\varphi ,\delta _k}$
and
$F \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\varphi ,\delta _k}$
and
![]() $k \in K_{s^k, F}$
, then
$k \in K_{s^k, F}$
, then
![]() $\varphi (\bigcup _{n} F_{k_n})<\varepsilon _k$
. Without loss of generality, we can assume that
$\varphi (\bigcup _{n} F_{k_n})<\varepsilon _k$
. Without loss of generality, we can assume that
![]() $\delta _{k+1}<\delta _k<\varepsilon _k$
. Let us define
$\delta _{k+1}<\delta _k<\varepsilon _k$
. Let us define
![]() $s=(s_n) \in \mathscr {H}$
as follows:
$s=(s_n) \in \mathscr {H}$
as follows:
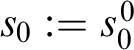 $s_0:=s_0^0$
and, for each
$s_0:=s_0^0$
and, for each
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $s_{n+1}$
be such that for all
$s_{n+1}$
be such that for all
![]() $m\leq n+1$
there is
$m\leq n+1$
there is
![]() $\ell \in \omega $
such that
$\ell \in \omega $
such that
![]() $s_n\leq s^m_\ell <s_{n+1}$
. Then, set
$s_n\leq s^m_\ell <s_{n+1}$
. Then, set
![]() $S_0:=[0,s_0]$
and
$S_0:=[0,s_0]$
and
![]() $S_{n+1}:=(s_{n},s_{n+1}]$
for all
$S_{n+1}:=(s_{n},s_{n+1}]$
for all
![]() $n\in \omega $
.
$n\in \omega $
.
Also, let
![]() $\psi $
be the lscsm defined by
$\psi $
be the lscsm defined by
![]() $\psi (\emptyset )=0$
and, for each nonempty
$\psi (\emptyset )=0$
and, for each nonempty
![]() $A\subseteq \omega $
,
$A\subseteq \omega $
,
![]() $\psi (A):=\delta _k$
, where k is the minimal integer such that
$\psi (A):=\delta _k$
, where k is the minimal integer such that
![]() $A\cap S_k\neq \emptyset $
. At this point, set
$A\cap S_k\neq \emptyset $
. At this point, set
![]() $\nu :=\max \{\varphi ,\psi \}$
. Then
$\nu :=\max \{\varphi ,\psi \}$
. Then
![]() $\nu $
is a lscsm such that
$\nu $
is a lscsm such that
![]() $\mathrm {Exh}(\nu )=\mathrm {Exh}(\varphi )$
. Indeed, on the one hand,
$\mathrm {Exh}(\nu )=\mathrm {Exh}(\varphi )$
. Indeed, on the one hand,
![]() $\nu \geq \varphi $
, hence
$\nu \geq \varphi $
, hence
![]() $\mathrm {Exh}(\nu )\subseteq \mathrm {Exh}(\varphi )$
. On the other hand, fix
$\mathrm {Exh}(\nu )\subseteq \mathrm {Exh}(\varphi )$
. On the other hand, fix
![]() $A\in \mathrm {Exh}(\varphi )$
and
$A\in \mathrm {Exh}(\varphi )$
and
![]() $\varepsilon>0$
, hence there is
$\varepsilon>0$
, hence there is
![]() $n_0\in \omega $
such that
$n_0\in \omega $
such that
![]() $\mu (A\setminus n)<\varepsilon $
for all
$\mu (A\setminus n)<\varepsilon $
for all
![]() $n\geq n_0$
. Also, there is
$n\geq n_0$
. Also, there is
![]() $n_1\in \omega $
such that
$n_1\in \omega $
such that
![]() $\delta _n<\varepsilon $
for all
$\delta _n<\varepsilon $
for all
![]() $n\geq n_1$
. Thus, for each n such that
$n\geq n_1$
. Thus, for each n such that
![]() $n\geq n_0$
and
$n\geq n_0$
and
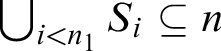 $\bigcup _{i<n_1}S_i\subseteq n$
we have
$\bigcup _{i<n_1}S_i\subseteq n$
we have
![]() $\nu (A\setminus n)<\varepsilon $
. Therefore
$\nu (A\setminus n)<\varepsilon $
. Therefore
![]() $A\in \mathrm {Exh}(\nu )$
, which proves the opposite inclusion
$A\in \mathrm {Exh}(\nu )$
, which proves the opposite inclusion
![]() $\mathrm {Exh}(\varphi )\subseteq \mathrm {Exh}(\nu )$
.
$\mathrm {Exh}(\varphi )\subseteq \mathrm {Exh}(\nu )$
.
Lastly, we show that
![]() $\nu $
satisfies the condition in the statement. Fix
$\nu $
satisfies the condition in the statement. Fix
![]() $\varepsilon>0$
and let m be the minimal integer such that
$\varepsilon>0$
and let m be the minimal integer such that
![]() $\varepsilon _m\leq \varepsilon $
. We claim that
$\varepsilon _m\leq \varepsilon $
. We claim that
![]() $\delta :=\delta _m$
witnesses this condition. Fix
$\delta :=\delta _m$
witnesses this condition. Fix
![]() $(F_n) \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\nu ,\delta }$
,
$(F_n) \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\nu ,\delta }$
,
![]() $k \in K_{s,F}$
, and
$k \in K_{s,F}$
, and
![]() $j\in \omega $
. Then there exist
$j\in \omega $
. Then there exist
![]() $\ell ^\prime ,\ell ^{\prime \prime } \in \omega $
such that
$\ell ^\prime ,\ell ^{\prime \prime } \in \omega $
such that
 $$ \begin{align*}\max F_{k_{2j}}\leq s_{\ell^\prime}<\min F_{k_{2j+1}}\leq\max F_{k_{2j+1}}\leq s_{\ell^{\prime\prime}}<\min F_{k_{2(j+1)}}. \end{align*} $$
$$ \begin{align*}\max F_{k_{2j}}\leq s_{\ell^\prime}<\min F_{k_{2j+1}}\leq\max F_{k_{2j+1}}\leq s_{\ell^{\prime\prime}}<\min F_{k_{2(j+1)}}. \end{align*} $$
Note that
![]() $m<\ell ^\prime <\ell ^{\prime \prime }$
, where the former inequality follows by the fact that
$m<\ell ^\prime <\ell ^{\prime \prime }$
, where the former inequality follows by the fact that
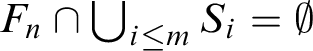 $F_n \cap \bigcup _{i\le m}S_i =\emptyset $
for all n (by the definition of
$F_n \cap \bigcup _{i\le m}S_i =\emptyset $
for all n (by the definition of
![]() $\nu $
and the hypothesis
$\nu $
and the hypothesis
![]() $(F_n) \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\nu ,\delta }$
) and the latter since
$(F_n) \in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\nu ,\delta }$
) and the latter since
![]() $s\in \mathscr {H}$
. Thus, there exists
$s\in \mathscr {H}$
. Thus, there exists
![]() $\ell \in \omega $
such that
$\ell \in \omega $
such that
It follows that
 $\max F_{k_{2j}}\leq s^m_{\ell }<\min F_{k_{2(j+1)}}$
, so that
$\max F_{k_{2j}}\leq s^m_{\ell }<\min F_{k_{2(j+1)}}$
, so that
![]() $(k_{2n})\in K_{s^m, F}$
. Therefore
$(k_{2n})\in K_{s^m, F}$
. Therefore
![]() $\varphi (\bigcup _{n} F_{k_{2n}})<\varepsilon _m\leq \varepsilon $
. It is also easy to see that
$\varphi (\bigcup _{n} F_{k_{2n}})<\varepsilon _m\leq \varepsilon $
. It is also easy to see that
![]() $\psi (\bigcup _{n} F_{k_{2n}})\leq \delta =\delta _m<\varepsilon _m\leq \varepsilon $
. Putting all together, we conclude that
$\psi (\bigcup _{n} F_{k_{2n}})\leq \delta =\delta _m<\varepsilon _m\leq \varepsilon $
. Putting all together, we conclude that
![]() $\nu (\bigcup _{n} F_{k_{2n}})<\varepsilon $
.⊣
$\nu (\bigcup _{n} F_{k_{2n}})<\varepsilon $
.⊣
Lemma 5.6. Let
![]() $\nu $
be a lscsm as in Lemma 5.5. Then
$\nu $
be a lscsm as in Lemma 5.5. Then
![]() $\mathrm {Exh}(\nu )$
is a generalized density ideal.
$\mathrm {Exh}(\nu )$
is a generalized density ideal.
Proof. Define
![]() $S_0:=[0,s_0]$
and
$S_0:=[0,s_0]$
and
![]() $S_{n+1}:=(s_n,s_{n+1}]$
for all
$S_{n+1}:=(s_n,s_{n+1}]$
for all
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $\boldsymbol {\mu }=(\mu _n)$
be the sequence of lscsms defined by
$\boldsymbol {\mu }=(\mu _n)$
be the sequence of lscsms defined by
We claim that
![]() $\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})=\mathrm {Exh}(\nu )$
, where
$\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})=\mathrm {Exh}(\nu )$
, where
![]() $\varphi _{\boldsymbol {\mu }}:=\sup _n \mu _n$
.
$\varphi _{\boldsymbol {\mu }}:=\sup _n \mu _n$
.
It is clear that
![]() $\varphi _{\boldsymbol {\mu }} \le \nu $
, hence
$\varphi _{\boldsymbol {\mu }} \le \nu $
, hence
![]() $\mathrm {Exh}(\nu )\subseteq \mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
. Conversely, fix
$\mathrm {Exh}(\nu )\subseteq \mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
. Conversely, fix
![]() $A\in \mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
and
$A\in \mathrm {Exh}(\varphi _{\boldsymbol {\mu }})$
and
![]() $\varepsilon>0$
, hence there is
$\varepsilon>0$
, hence there is
![]() $\delta>0$
such that, if
$\delta>0$
such that, if
![]() $F=(F_n)\in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\nu ,\delta }$
and
$F=(F_n)\in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\nu ,\delta }$
and
![]() $k\in K_{s,F}$
, then
$k\in K_{s,F}$
, then
![]() . There exists
. There exists
![]() $n_0\in \omega $
such that
$n_0\in \omega $
such that
![]() $\mu _n(A)<\delta $
for all
$\mu _n(A)<\delta $
for all
![]() $n\geq n_0$
. Define
$n\geq n_0$
. Define
![]() $F_n:=A\cap S_{n+n_0}$
for all
$F_n:=A\cap S_{n+n_0}$
for all
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $\nu (F_n)=\mu _{n+n_0}(A)<\delta $
for all
$\nu (F_n)=\mu _{n+n_0}(A)<\delta $
for all
![]() $n \in \omega $
. Thus
$n \in \omega $
. Thus
![]() $(F_n)\in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\nu ,\delta }$
and for each
$(F_n)\in \mathcal {F}_{\mathrm {incr}} \cap \mathcal {G}_{\nu ,\delta }$
and for each
![]() $k \in K_{s,F}$
we have
$k \in K_{s,F}$
we have
![]() . Note the sequences
. Note the sequences
![]() $(n)$
and
$(n)$
and
![]() $(n+1)$
belong to
$(n+1)$
belong to
![]() $K_{s,F}$
, so that
$K_{s,F}$
, so that
![]() and
and
![]() . Define
. Define
![]() $m:=\min S_{n_0}$
. Then for each
$m:=\min S_{n_0}$
. Then for each
![]() $m\geq m_0$
we have
$m\geq m_0$
we have
 $$ \begin{align*}\nu(A\setminus m) \le \nu(A\setminus m_0)=\nu\left(\bigcup_{n \in \omega} F_n\right) \le \nu\left(\bigcup_{n\in \omega} F_{2n}\right)+\nu\left(\bigcup_{n\in \omega} F_{2n+1}\right) <\varepsilon. \end{align*} $$
$$ \begin{align*}\nu(A\setminus m) \le \nu(A\setminus m_0)=\nu\left(\bigcup_{n \in \omega} F_n\right) \le \nu\left(\bigcup_{n\in \omega} F_{2n}\right)+\nu\left(\bigcup_{n\in \omega} F_{2n+1}\right) <\varepsilon. \end{align*} $$
We conclude that
![]() $A\in \mathrm {Exh}(\nu )$
, therefore
$A\in \mathrm {Exh}(\nu )$
, therefore
![]() $\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})\subseteq \mathrm {Exh}(\nu )$
.⊣
$\mathrm {Exh}(\varphi _{\boldsymbol {\mu }})\subseteq \mathrm {Exh}(\nu )$
.⊣
We are finally ready to prove Theorem 5.3, cf. Figure 1 below.
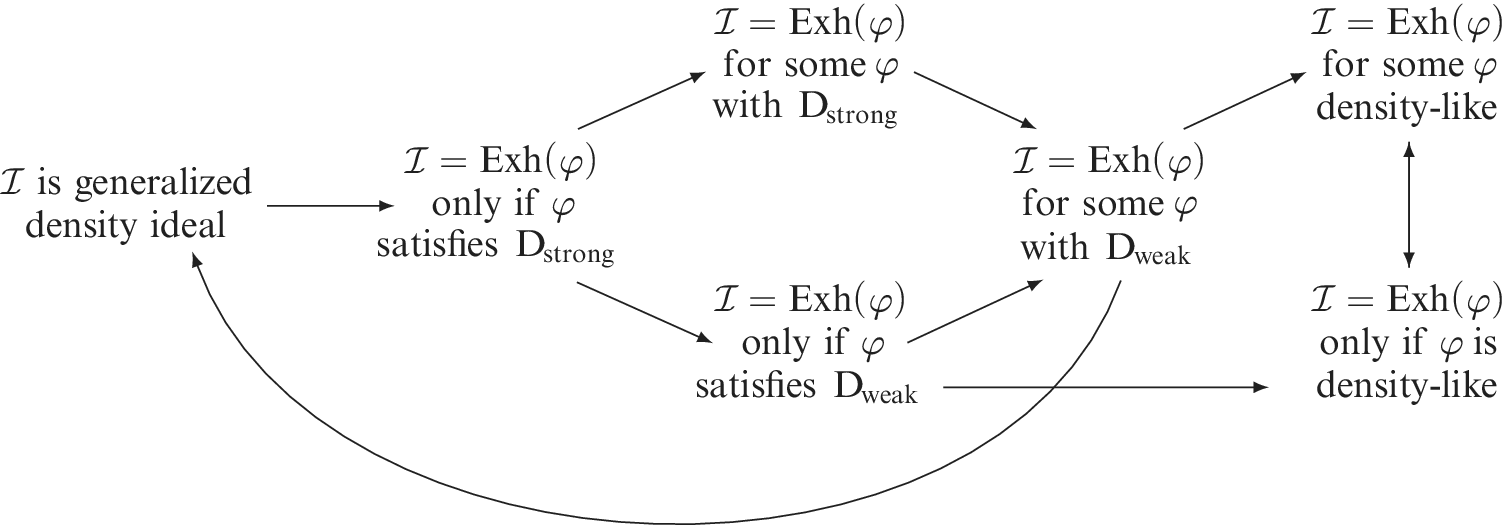
Figure 1 Relationship between generalized density ideals and density-like ideals, assuming
![]() $\mathcal {I}$
is an analytic P-ideal.
$\mathcal {I}$
is an analytic P-ideal.
6 Concluding remarks
Differently from the case of density-like lscsms, if
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are two lscsms such that
$\psi $
are two lscsms such that
![]() $\mathrm {Exh}(\varphi )=\mathrm {Exh}(\psi )$
and
$\mathrm {Exh}(\varphi )=\mathrm {Exh}(\psi )$
and
![]() $\varphi $
is strongly-density-like, then
$\varphi $
is strongly-density-like, then
![]() $\psi $
is not necessarily strongly-density-like.
$\psi $
is not necessarily strongly-density-like.
Indeed, let
![]() $\varphi $
be the strongly-density-like lscsm defined in Example 4.6. Then, with the same notations, it is easily seen that
$\varphi $
be the strongly-density-like lscsm defined in Example 4.6. Then, with the same notations, it is easily seen that
![]() $A\in \mathrm {Exh}(\varphi )$
if and only if
$A\in \mathrm {Exh}(\varphi )$
if and only if
![]() $A\cap X_n\in \mathrm {Fin}$
for all
$A\cap X_n\in \mathrm {Fin}$
for all
![]() $n \in \omega $
, hence
$n \in \omega $
, hence
![]() $\mathrm {Exh}(\varphi )$
is isomorphic to
$\mathrm {Exh}(\varphi )$
is isomorphic to
![]() $\emptyset \times \mathrm {Fin}$
. However,
$\emptyset \times \mathrm {Fin}$
. However,
![]() $\emptyset \times \mathrm {Fin}$
is a generalized density ideal and, thanks to Remark 4.5, there exists a strongly-density-like lscsm
$\emptyset \times \mathrm {Fin}$
is a generalized density ideal and, thanks to Remark 4.5, there exists a strongly-density-like lscsm
![]() $\psi $
such that
$\psi $
such that
![]() $\mathrm {Exh}(\varphi )=\mathrm {Exh}(\psi )$
. We conclude with an open question.
$\mathrm {Exh}(\varphi )=\mathrm {Exh}(\psi )$
. We conclude with an open question.
Question 5. Does there exist a density-like ideal
![]() $\mathcal {I}$
such that
$\mathcal {I}$
such that
![]() $\mathcal {I}\neq \mathrm {Exh}(\varphi )$
for each strongly-density-like lscsm
$\mathcal {I}\neq \mathrm {Exh}(\varphi )$
for each strongly-density-like lscsm
![]() $\varphi $
?
$\varphi $
?
Acknowledgments
The authors are grateful to an anonymous reviewer for his careful reading of the manuscript and constructive suggestions, and to Jacek Tryba (University of Gdańsk, PL) for several useful comments and for pointing out reference [Reference Oliver20]. P.L. thanks PRIN 2017 (grant no. 2017CY2NCA) for financial support.