Article contents
Descriptive complexity of finite structures: Saving the quantifier rank
Published online by Cambridge University Press: 12 March 2014
Abstract
We say that a first order formula Φ distinguishes a structure M over a vocabulary L from another structure M′ over the same vocabulary if Φ is true on M but false on M′. A formula Φ defines an L-structure M if Φ distinguishes M from any other non-isomorphic L-structure M′. A formula Φ identifies an n-element L-structure M if Φ distinguishes M from any other non-isomorphic n-element L-structure M′.
We prove that every n-element structure M is identifiable by a formula with quantifier rank less than 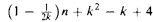 and at most one quantifier alternation, where k is the maximum relation arity of M. Moreover, if the automorphism group of M contains no transposition of two elements, the same result holds for definability rather than identification.
and at most one quantifier alternation, where k is the maximum relation arity of M. Moreover, if the automorphism group of M contains no transposition of two elements, the same result holds for definability rather than identification.
The Bernays-Schönfinkel class consists of prenex formulas in which the existential quantifiers all precede the universal quantifiers. We prove that every n-element structure M is identifiable by a formula in the Bernays-Schönfinkel class with less than 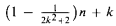 quantifiers. If in this class of identifying formulas we restrict the number of universal quantifiers to k, then less than
quantifiers. If in this class of identifying formulas we restrict the number of universal quantifiers to k, then less than 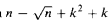 quantifiers suffice to identify M and. as long as we keep the number of universal quantifiers bounded by a constant, at total
quantifiers suffice to identify M and. as long as we keep the number of universal quantifiers bounded by a constant, at total  quantifiers are necessary.
quantifiers are necessary.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2005
References
REFERENCES
- 6
- Cited by

