Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T06:17:30.736Z Has data issue: false hasContentIssue false
  • English
  • Français

Determinateness of certain almost-Borel games

Published online by Cambridge University Press:  12 March 2014

Robert S. Wolf
Robert S. Wolf*
Affiliation:
Department of Mathematics, California Polytechnic, State University, San Luis Obispo, California 93407
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove (in ZFC Set Theory) that all infinite games whose winning sets are of the following forms are determined:

(1) (A − S) ∪ B, where A is 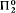, , 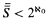and the game whose winning set is B is “strongly determined” (meaning that all of its subgames are determined).

(2) A Boolean combination of 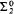sets and sets smaller than the continuum.

This also enables us to show that strong determinateness is not preserved under complementation, improving a result of Morton Davis which required the continuum hypothesis to prove this fact.

Various open questions related to the above results are discussed. Our main conjecture is that (2) above remains true when 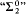is replaced by “Borel”.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 3 , September 1985 , pp. 569 - 579
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Davis, M., Infinite games with perfect information, Advances in games theory, Annals of Mathematics Studies, no. 52, Princeton University Press, Princeton, New Jersey, 1964, pp. 85–101.Google Scholar
[2]Fenstad, J. E., The axiom of determinateness, Logic Colloquium '69 (Gandy, R. O. and Yates, C. P., editors), North-Holland, Amsterdam, 1971, pp. 41–61.Google Scholar
[3]Gale, D. and Stewart, F. M., Infinite games with perfect information, Contributions to the Theory of Garnet, Annals of Mathematics Studies, no. 28, Princeton University Press, Princeton, New Jersey, 1953, pp. 245–266.Google Scholar
[4]Kuratowski, C., Topology. Vol. II, 4th ed., PWN, Warsaw, and Academic Press, New York, 1968.Google Scholar
[5]Martin, D. A., Borel determinacy, Annals of Mathematics, ser. 2, vol. 102 (1975), pp. 363–372.CrossRefGoogle Scholar
[6]Mycielski, J., On the axiom of determinateness, Fundament a Mathematkae, vol. 53 (1964), pp. 205–224.CrossRefGoogle Scholar