Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pila, Jonathan
2005.
Rational points on a subanalytic surface.
Annales de l'Institut Fourier,
Vol. 55,
Issue. 5,
p.
1501.
Pila, J.
and
Wilkie, A. J.
2006.
The rational points of a definable set.
Duke Mathematical Journal,
Vol. 133,
Issue. 3,
Mamino, Marcello
2014.
On the computing power of +, -, and ×.
p.
1.
Binyamini, Gal
2022.
Point counting for foliations over number fields.
Forum of Mathematics, Pi,
Vol. 10,
Issue. ,
Wilkie, Alex J.
2024.
Analytic continuation and Zilber’s quasiminimality
conjecture.
Model Theory,
Vol. 3,
Issue. 2,
p.
701.
Bhardwaj, Neer
McCulloch, Raymond
Ramachandran, Nandagopal
and
Woo, Katharine
2025.
INTEGER-VALUED O-MINIMAL FUNCTIONS.
The Quarterly Journal of Mathematics,
Vol. 76,
Issue. 2,
p.
715.

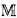 be an o-minimal expansion of the ordered field of real numbers
be an o-minimal expansion of the ordered field of real numbers 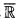 , and let
, and let 