No CrossRef data available.
Article contents
DISCONTINUOUS HOMOMORPHISMS OF 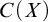 $C(X)$ WITH
$C(X)$ WITH 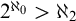 $2^{\aleph _0}>\aleph _2$
$2^{\aleph _0}>\aleph _2$
Published online by Cambridge University Press: 15 April 2024
Abstract
Assume that M is a transitive model of 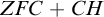 $ZFC+CH$ containing a simplified
$ZFC+CH$ containing a simplified 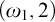 $(\omega _1,2)$-morass,
$(\omega _1,2)$-morass, 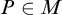 $P\in M$ is the poset adding
$P\in M$ is the poset adding 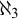 $\aleph _3$ generic reals and G is P-generic over M. In M we construct a function between sets of terms in the forcing language, that interpreted in
$\aleph _3$ generic reals and G is P-generic over M. In M we construct a function between sets of terms in the forcing language, that interpreted in 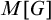 $M[G]$ is an
$M[G]$ is an 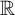 $\mathbb R$-linear order-preserving monomorphism from the finite elements of an ultrapower of the reals, over a non-principal ultrafilter on
$\mathbb R$-linear order-preserving monomorphism from the finite elements of an ultrapower of the reals, over a non-principal ultrafilter on 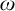 $\omega $, into the Esterle algebra of formal power series. Therefore it is consistent that
$\omega $, into the Esterle algebra of formal power series. Therefore it is consistent that  $2^{\aleph _0}>\aleph _2$ and, for any infinite compact Hausdorff space X, there exists a discontinuous homomorphism of
$2^{\aleph _0}>\aleph _2$ and, for any infinite compact Hausdorff space X, there exists a discontinuous homomorphism of  $C(X)$, the algebra of continuous real-valued functions on X.
$C(X)$, the algebra of continuous real-valued functions on X.
Keywords
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic


