Article contents
A discrete chain of degrees of index sets
Published online by Cambridge University Press: 12 March 2014
Extract
Let {Wi} be a standard enumeration of all recursively enumerable (r.e.) sets, and for any class A of r.e. sets, let θA denote the index set of A = {n ∣ Wn ∈ A}. (Clearly, 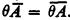 .) In [1], the index sets of nonempty finite classes of finite sets were classified under one-one reducibility into an increasing sequence {Ym}, 0 ≤ m < ∞. In this paper we examine further properties of this sequence within the partial ordering of one-one degrees of index sets. The main results are as follows: (1) For each m, Ym < Ym + 1 and
.) In [1], the index sets of nonempty finite classes of finite sets were classified under one-one reducibility into an increasing sequence {Ym}, 0 ≤ m < ∞. In this paper we examine further properties of this sequence within the partial ordering of one-one degrees of index sets. The main results are as follows: (1) For each m, Ym < Ym + 1 and 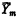 < Ym + 1; (2) Ym is incomparable to
< Ym + 1; (2) Ym is incomparable to 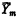 ; (3) Ym + 1 and
; (3) Ym + 1 and 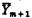 ; are immediate successors (among index sets) of Ym and
; are immediate successors (among index sets) of Ym and 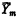 m; (4) the pair (Ym + 1,
m; (4) the pair (Ym + 1, 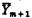 ) is a “least upper bound” for the pair (Ym,
) is a “least upper bound” for the pair (Ym, 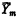 ) in the sense that any successor of both Ym and
) in the sense that any successor of both Ym and 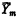 is ≥ Ym + 1or
is ≥ Ym + 1or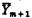 ; (5) the pair (Ym,
; (5) the pair (Ym, 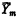 ) is a “greatest lower bound” for the pair (Ym + 1,
) is a “greatest lower bound” for the pair (Ym + 1, 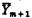 ) in the sense that any predecessor of both Ym + 1 and
) in the sense that any predecessor of both Ym + 1 and 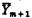 is ≤ Ym or
is ≤ Ym or 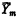 . Since
. Since 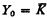 and all Ym are in the bounded truth-table degree of K, this yields some local information about the one-one degrees of index sets which are “at the bottom” in the one-one ordering of index sets.
and all Ym are in the bounded truth-table degree of K, this yields some local information about the one-one degrees of index sets which are “at the bottom” in the one-one ordering of index sets.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
References
REFERENCES
- 8
- Cited by

