Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mamane, Lionel Elie
2006.
Types for Proofs and Programs.
Vol. 3839,
Issue. ,
p.
170.

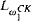 . This equivalence is used to answer several open questions concerning the metadyadics. Results obtained seem to indicate that the metadyadics best capture the notion of a recursive surreal number.
. This equivalence is used to answer several open questions concerning the metadyadics. Results obtained seem to indicate that the metadyadics best capture the notion of a recursive surreal number.