Article contents
Effectively nowhere simple sets
Published online by Cambridge University Press: 12 March 2014
Extract
An r.e. set A is nowhere simple if for every r.e. set We such that We − A is infinite, there is an infinite r.e. set W such that W ⊆ We − A. The definition of nowhere simple sets is due to R. Shore in [4]. In [4], Shore studied various properties of nowhere simple sets and showed that they could be used to give an elegant and simple proof of the fact that every nontrivial class of r.e. sets C closed under recursive isomorphisms is an automorphism base for 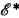 , the lattice of r.e. sets modulo finite sets, (that is, an automorphism α of
, the lattice of r.e. sets modulo finite sets, (that is, an automorphism α of 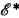 is completely determined by its action on C; see Theorem 8 of [4]). Shore also defined the notion of effectively nowhere simple sets.
is completely determined by its action on C; see Theorem 8 of [4]). Shore also defined the notion of effectively nowhere simple sets.
Definition. An r.e. set A is effectively nowhere simple if there is a recursive function f such that for every i, Wf(i) ⊆ Wi − A and Wf(i) is infinite iff Wi − A is infinite. f is called a witness function for A.
Other than to produce examples of effectively nowhere simple sets and nowhere simple sets that are not effectively nowhere simple, Shore did not concern himself with the properties of effectively nowhere simple sets since he felt that effectively nowhere simple sets were unlikely to be lattice invariant in either E, the lattice of r.e. sets, or in 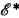 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
REFERENCES
- 6
- Cited by

