Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hutchinson, John E.
1976.
Model theory via set theory.
Israel Journal of Mathematics,
Vol. 24,
Issue. 3-4,
p.
286.
Barwise, Jon
Kaufmann, Matt
and
Makkai, Michael
1978.
Stationary logic.
Annals of Mathematical Logic,
Vol. 13,
Issue. 2,
p.
171.
Kotlarski, Henryk
1980.
On Skolem Ultrapowers and Their Non‐Standard Variant.
Mathematical Logic Quarterly,
Vol. 26,
Issue. 14-18,
p.
227.
Enayat, Ali
1984.
On certain elementary extensions of models of set theory.
Transactions of the American Mathematical Society,
Vol. 283,
Issue. 2,
p.
705.
Baldwin, John T.
and
Larson, Paul B.
2016.
Iterated elementary embeddings and the model theory of infinitary logic.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 3,
p.
309.

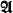 is a countable model of ZFC and
is a countable model of ZFC and 