Article contents
Elimination of extra-logical postulates
Published online by Cambridge University Press: 12 March 2014
Extract
Under certain circumstances a postulate can be eliminated in favor of a mere definition, or convention of notational abbreviation. Suppose e.g. that a given system presupposes the machinery of ordinary logic and contains in addition a single extra-logical primitive: the relation Pt, “is a spatial part of.” Suppose this relation is governed by a single extra-logical postulate, to the effect that Pt is transitive:
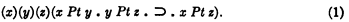
Now instead of Pt, the relation O of spatial overlapping might be taken as primitive; Pt could then be defined in terms of O as follows:
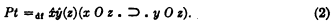
The transitivity of Pt then follows by purely logical principles from the definition. The statement (1) with its ‘Pt’ clauses expanded according to (2) is a purely logical theorem, demonstrable independently of any stipulations or assumptions concerning the properties of O. Thus, through a change involving neither increase nor decrease of primitive ideas, the need of adopting (1) as a postulate is removed.
Or again, consider a system comprising ordinary logic and the sole extra-logical primitive S, the relation of simultaneity, governed by a sole postulate to the effect that S is symmetrical:
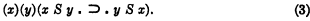
Here instead of S the relation N, “is no later than” might be taken as primitive; S could then be defined in terms of N as follows:
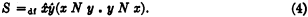
Postulation of (3) then becomes unnecessary, for (3) is an abbreviation, according to (4), of a theorem which is demonstrable within pure logic.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1940
References
1 For one such theory and citations of others see Quine, , Mathematical logic (W. W. Norton A Co., 1940), pp. 128–132, 155–160, 162–166Google Scholar.
2 Cf. Leonard, and Goodman, , A calculus of individuals, this Journal, vol. 5 (1940), pp. 48–49Google Scholar. The postulates of that paper are here rendered in unabbreviated form, and so recast as not to depend on the theory of types. On abandonment of the theory of types the range of ‘x’, ‘y’, etc. ceases to be limited to individuals; hence we find ourselves called upon to decide whether to construe ![]() as vacuously true or as false when x and y are not both individuals. We here arbitrarily adopt the former alternative; thus the clause
as vacuously true or as false when x and y are not both individuals. We here arbitrarily adopt the former alternative; thus the clause ![]() in (13) and (14) stipulates that x is an individual.
in (13) and (14) stipulates that x is an individual.
3 The latter notion, under the name ‘completeness relative to logic,’ is due to Tarski. It is easier to formulate than the older concept of categoricity, and is related to the latter as follows: systems which are categorical (with respect to a given logic) are synthetically complete, and synthetically complete systems possessed of logical models are categorical. These matters were set forth by Tarski at the Harvard Logic Club in January, 1940, and will appear in a paper On completeness and categoricity of deductive theories. See also Lindenbaum, and Tarski, , Über die Beschränktheit der Ausdrucksmittel deduktiver Theorien, Ergebnisse eines mathematischen Kolloquiums, Heft 7 (1936), pp. 15–22Google Scholar, wherein ‘Nichtgabelbarkeit’ answers to ‘synthetic completeness.’
- 4
- Cited by

