Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T17:25:46.548Z Has data issue: false hasContentIssue false
  • English
  • Français

Elimination of quantifiers for ordered valuation rings

Published online by Cambridge University Press:  12 March 2014

M. A. Dickmann
M. A. Dickmann*
Affiliation:
Equipe de Logique Mathématique, U. E. R. De Mathématique et Informatique, Universite Paris VII, Paris, France
Get access Rights & Permissions [Opens in a new window]

Extract

Cherlin and Dickmann [2] proved that the theory RCVR of real closed (valuation) rings admits quantifier-elimination (q.e.) in the language ℒ = {+, −, ·, 0, 1, <, ∣} for ordered rings augmented by the divisibility relation “∣”. The purpose of this paper is to prove a form of converse of this result:

Theorem. Let T be a theory of ordered commutative domains (which are not fields), formulated in the language ℒ. In addition we assume that:

  • (1) The symbol “∣” is interpreted as the honest divisibility relation:

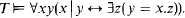
  • (2) The following divisibility property holds in T:

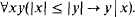
If T admits q.e. in ℒ, then T = RCVR.

We do not know at present whether the restriction imposed by condition (2) can be weakened.

The divisibility property (DP) has been considered in the context of ordered valued fields; see [4] for example. It also appears in [2], and has been further studied in Becker [1] from the point of view of model theory. Ordered domains in which (DP) holds are called in [1] convexly ordered valuation rings, for reasons which the proposition below makes clear. The following summarizes the basic properties of these rings:

Proposition I [2, Lemma 4]. (1) Let A be a linearly ordered commutative domain. The following are equivalent:

  • (a) A is a convexly ordered valuation ring.

  • (b) Every ideal (or, equivalently, principal ideal) is convex in A.

  • (c) A is a valuation ring convex in its field of fractions quot(A).

  • (d) A is a valuation ring and its maximal ideal MA is convex (in A or, equivalently, in quot (A)).

  • (e) A is a valuation ring and its maximal ideal is bounded by ± 1.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 52 , Issue 1 , March 1987 , pp. 116 - 128
Copyright
Copyright © Association for Symbolic Logic 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Becker, T., Real closed rings and ordered valuation rings, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 29 (1983), pp. 417–425.CrossRefGoogle Scholar
[2] Cherlin, G. and Dickmann, M. A., Real closed rings. II: Model theory, Annals of Pure and Applied Logic, vol. 25 (1983), pp. 213–231.CrossRefGoogle Scholar
[3] Delon, F., Quelques propriétés des corps values en théorie des modèles, Thèse de Doctorat d'État, Université Paris VII, Paris, 1982.Google Scholar
[4] Knebusch, M. and Wright, M. J., Bewertungen mit reeller Henselisierung, Journal für die Reine und Angewandte Mathematik, vol. 286/287 (1976), pp. 314–321.Google Scholar
[5] Macintyre, A., McKenna, K. and van den Dries, L., Elimination of quantifiers in algebraic structures, Advances in Mathematics, vol. 47 (1983), pp. 74–87.CrossRefGoogle Scholar
[6] Pillay, A. and Steinhorn, C., Definable sets in ordered structures. I, Transactions of the American Mathematical Society, vol. 295 (1986), pp. 565–592.CrossRefGoogle Scholar
[7] van den Dries, L., A linearly ordered ring whose theory admits quantifier elimination is a real closed field, Proceedings of the American Mathematical Society, vol. 79 (1980), pp. 97–100.CrossRefGoogle Scholar