Article contents
ENAYAT MODELS OF PEANO ARITHMETIC
Published online by Cambridge University Press: 21 December 2018
Abstract
Simpson [6] showed that every countable model 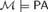 ${\cal M} \models PA$ has an expansion
${\cal M} \models PA$ has an expansion 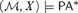 $\left( {{\cal M},X} \right) \models P{A^{\rm{*}}}$ that is pointwise definable. A natural question is whether, in general, one can obtain expansions of a nonprime model in which the definable elements coincide with those of the underlying model. Enayat [1] showed that this is impossible by proving that there is
$\left( {{\cal M},X} \right) \models P{A^{\rm{*}}}$ that is pointwise definable. A natural question is whether, in general, one can obtain expansions of a nonprime model in which the definable elements coincide with those of the underlying model. Enayat [1] showed that this is impossible by proving that there is  ${\cal M} \models PA$ such that for each undefinable class X of
${\cal M} \models PA$ such that for each undefinable class X of  ${\cal M}$, the expansion
${\cal M}$, the expansion 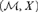 $\left( {{\cal M},X} \right)$ is pointwise definable. We call models with this property Enayat models. In this article, we study Enayat models and show that a model of
$\left( {{\cal M},X} \right)$ is pointwise definable. We call models with this property Enayat models. In this article, we study Enayat models and show that a model of 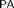 $PA$ is Enayat if it is countable, has no proper cofinal submodels and is a conservative extension of all of its elementary cuts. We then show that, for any countable linear order γ, if there is a model
$PA$ is Enayat if it is countable, has no proper cofinal submodels and is a conservative extension of all of its elementary cuts. We then show that, for any countable linear order γ, if there is a model 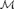 ${\cal M}$ such that
${\cal M}$ such that 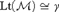 $Lt\left( {\cal M} \right) \cong \gamma$, then there is an Enayat model
$Lt\left( {\cal M} \right) \cong \gamma$, then there is an Enayat model 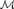 ${\cal M}$ such that
${\cal M}$ such that 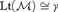 $Lt\left( {\cal M} \right) \cong \gamma$.
$Lt\left( {\cal M} \right) \cong \gamma$.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2018
References
REFERENCES
- 1
- Cited by

