Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Arai, Toshiyasu
2011.
Exact bounds on epsilon processes.
Archive for Mathematical Logic,
Vol. 50,
Issue. 3-4,
p.
445.
ARAI, Toshiyasu
2012.
A Sneak Preview of Proof Theory of Ordinals(<Special Section>Infinity in Philosophy and Mathematics).
Annals of the Japan Association for Philosophy of Science,
Vol. 20,
Issue. 0,
p.
29.
ARAI, TOSHIYASU
2013.
PROOF THEORY OF WEAK COMPACTNESS.
Journal of Mathematical Logic,
Vol. 13,
Issue. 01,
p.
1350003.
Towsner, Henry
2018.
Epsilon substitution for $$\textit{ID}_1$$ ID 1 via cut-elimination.
Archive for Mathematical Logic,
Vol. 57,
Issue. 5-6,
p.
497.

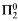 -FIX
-FIX