Article contents
Equality and lyndon's interpolation theorem
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper, we remark on some properties of equality that tend to be neglected and use them to give a proof of an extension of Lyndon's interpolation theorem. Let LK be a first order classical predicate calculus and LK= a first order classical predicate calculus with equality. We assume that LK and LK= have the propositional constant Τ (truth). For each formula F in LK=, let Rel+ (F), Rel− (F), Rel(F), and Fun(F) be the set of all the predicate symbols which occur in F positively, the set of all the predicate symbols which occur in F negatively, the set of all the predicate symbols which occur in F, and the set of all the function symbols which occur in F.
Theorem A (Lyndon [5]). Suppose that A and B are sentences in LK such that A ⊃ B is provable in LK. Then there is a sentence C in LK such that:
(i) A ⊃ C and C ⊃ B are provable in LK;
(ii) 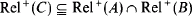 and
and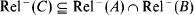
(iii) 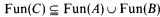 .
.
The sentence C which satisfies (i), (ii), (iii) in Theorem A is said to be an interpolant for A ⊃ B in Theorem A. Note that condition (iii) is not included in the original form of Lyndon's interpolation theorem (cf. [5]), but we can easily add this condition. Also, there is some obscurity in the original formulation with regard to the equality symbol. For example, Lyndon writes: “The theorem takes the same form whether or not we admit a predicate denoting identity, with suitable axioms, to the predicate calculus” [5, p. 129].
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
REFERENCES
- 4
- Cited by

