Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Downey, Rod
Hirschfeldt, Denis R.
Nies, André
and
Terwijn, Sebastiaan A.
2006.
Calibrating Randomness.
Bulletin of Symbolic Logic,
Vol. 12,
Issue. 3,
p.
411.
Miller, Joseph S.
and
Nies, André
2006.
Randomness and Computability: Open Questions.
Bulletin of Symbolic Logic,
Vol. 12,
Issue. 3,
p.
390.
Merkle, Wolfgang
and
Stephan, Frank
2007.
On C-Degrees, H-Degrees and T-Degrees.
p.
60.
Miller , Joseph S.
2009.
The K-Degrees, Low for K Degrees,and Weakly Low for K Sets.
Notre Dame Journal of Formal Logic,
Vol. 50,
Issue. 4,
Hölzl, Rupert
Kräling, Thorsten
Stephan, Frank
and
Wu, Guohua
2010.
Theoretical Computer Science.
Vol. 323,
Issue. ,
p.
259.
Conidis, Chris J.
2012.
Effectively approximating measurable sets by open sets.
Theoretical Computer Science,
Vol. 428,
Issue. ,
p.
36.
Barmpalias, George
2013.
Algorithmic Randomness and Measures of Complexity.
The Bulletin of Symbolic Logic,
Vol. 19,
Issue. 3,
p.
318.
Hölzl, Rupert
Kräling, Thorsten
Stephan, Frank
and
Wu, Guohua
2014.
Initial segment complexities of randomness notions.
Information and Computation,
Vol. 234,
Issue. ,
p.
57.
Downey, Rod
2014.
Turing's Legacy.
p.
90.
Bauwens, Bruno
2015.
Prefix and plain Kolmogorov complexity characterizations of 2-randomness: simple proofs.
Archive for Mathematical Logic,
Vol. 54,
Issue. 5-6,
p.
615.
Moser, Philippe
and
Stephan, Frank
2015.
Fundamentals of Computation Theory.
Vol. 9210,
Issue. ,
p.
81.
Bienvenu, Laurent
Desfontaines, Damien
and
Shen, Alexander
2015.
Automata, Languages, and Programming.
Vol. 9134,
Issue. ,
p.
219.
Bauwens, Bruno
2016.
Relating and Contrasting Plain and Prefix Kolmogorov Complexity.
Theory of Computing Systems,
Vol. 58,
Issue. 3,
p.
482.
Miyabe, Kenshi
2018.
Coherence of Reducibilities with Randomness Notions.
Theory of Computing Systems,
Vol. 62,
Issue. 7,
p.
1599.
Downey, Rod
and
Hirschfeldt, Denis R.
2019.
Algorithmic randomness.
Communications of the ACM,
Vol. 62,
Issue. 5,
p.
70.
Allender, Eric
Balaji, Nikhil
Datta, Samir
and
Pratap, Rameshwar
2023.
On the complexity of algebraic numbers, and the bit-complexity of straight-line programs.
Computability,
Vol. 12,
Issue. 2,
p.
145.

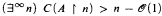 . where
. where 