Article contents
Extending the Curry-Howard interpretation to linear, relevant and other resource logics1
Published online by Cambridge University Press: 12 March 2014
Extract
The so-called Curry-Howard interpretation (Curry [1934], Curry and Feys [1958], Howard [1969], Tait [1965]) is known to provide a rather neat term-functional account of intuitionistic implication. Could one refine the interpretation to obtain an almost as good account of other neighbouring implications, including the so-called ‘resource’ implications (e.g. linear, relevant, etc.)?
We answer this question positively by demonstrating that just by working with side conditions on the rule of assertability conditions for the connective representing implication (‘→’) one can characterise those ‘resource’ logics. The idea stems from the realisation that whereas the elimination rule for conditionals (of which implication is a particular case) remains virtually unchanged no matter what kind of conditional one has (i.e. linear, relevant, intuitionistic, classical, etc., all have modus ponens), the corresponding introduction rule carries an element of vagueness which can be explored in the characterisation of several sorts of conditionals. The rule of →-introduction is classified as an ‘improper’ inference rule, to use a terminology from Prawitz [1965]. Now, the so-called improper rules leave room for manoeuvre as to how a particular logic can be obtained just by imposing conditions on the discharge of assumptions that would correspond to the particular logical discipline one is adopting (linear, relevant, ticket entailment, intuitionistic, classical, etc.). The side conditions can be ‘naturally’ imposed, given that a degree of ‘vagueness’ is introduced by the presentation of those improper inference rules, such as the rule of →-introduction:
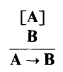
which says: starting from assumption ‘A’, and arriving at ‘B’ via an unspecified number of steps, one can discharge the assumption and conclude that ‘A’ implies ‘B’.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1992
Footnotes
A preliminary version of this paper was presented at the Informal Logic Colloquium, held at the Seminar für Natürlich-sprachliche Systeme (SNS), Universität Tübingen, on March 21–22, 1990, and has appeared in one volume of the series SNS-Berichte edited by P. Schroeder-Heister. Later, a more developed version was presented at Logic Colloquium '90, the European Summer Meeting of the Association for Symbolic Logic, Helsinki, Finland, July 15–22, 1990, the abstract of which appeared in this Journal, vol. 56(1991), pp. 1139–1140.
References
REFERENCES
- 38
- Cited by

