Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T20:06:39.120Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FIELD OF p-ADIC NUMBERS WITH A PREDICATE FOR THE POWERS OF AN INTEGER

Published online by Cambridge University Press:  21 March 2017

NATHANAËL MARIAULE
NATHANAËL MARIAULE*
Affiliation:
INSTITUT DE MATHÉMATIQUES DE JUSSIEU - PARIS RIVE GAUCHE UNIVERSITÉ PARIS DIDEROT 75205 PARIS CEDEX 13, FRANCEE-mail: nathanael.mariaule@imj-prg.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove the decidability of the theory of ℚp in the language (+, −,⋅, 0, 1, Pn(n ∈ ℕ)) expanded by a predicate for the multiplicative subgroup nℤ (where n is a fixed integer). There are two cases: if 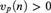$v_p \left( n \right) > 0$ then the group determines a cross-section and we get an axiomatization of the theory and a result of quantifier elimination. If 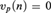$v_p \left( n \right) = 0$, then we use the Mann property of the group to get an axiomatization of the theory.

Keywords

p-adically closed fieldsexpansion of valued fields
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 1 , March 2017 , pp. 166 - 182
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Belegradek, O. and Zilber, B., The model theory of the field of reals with a subgroup of the unit circle . Journal of the London Mathematical Society, vol. 78 (2008), no. 3, pp. 563–579.Google Scholar
Evertse, J. H., On sums of S-units and linear recurrences . Composition Mathematica, vol. 53 (1984), no. 2, pp. 225–244.Google Scholar
Guignot, F., Théorie des modèles du groupe valué (ℤ, +, vp ), Séminaires de structures algébriques ordonnées, no. 89 (2014), preprint.Google Scholar
Günaydin, A. and van den Dries, L., The fields of real and complex numbers with a small multiplicative group . Proceedings of the London Mathematical Society, vol. 93 (2006), no. 1, pp. 43–81.Google Scholar
Lang, S., Algebra, third ed., Springer, Berlin, 2002.CrossRefGoogle Scholar
Laurent, M., Équations diophantiennes exponentielles . Inventiones Mathematicae, vol. 78 (1984), pp. 299–327.Google Scholar
Mann, H., On linear relations between roots of unity . Mathematika, vol. 12 (1965), pp. 101–117.Google Scholar
Prestel, A. and Roquette, P., Formally P-adic fields, Springer, Berlin, 1984.CrossRefGoogle Scholar
Robinson, A. and Zakon, E., Elementary properties of ordered abelian groups . Transactions of the American Mathematical Society, vol. 96 (1960), pp. 222–236.Google Scholar
van den Dries, L., The field of reals with a predicate for the powers of two . Manuscripta mathematica, vol. 54 (1985), pp. 187–195.Google Scholar
van der Poorten, A. J. and Schlickewei, H.P., Additive relations in fields . Journal of the Australian Mathematical Society, vol. 51 (1991), pp. 154–170.Google Scholar
Zakon, E., Generalized archimedean groups . Transactions of the American Mathematical Society, vol. 99 (1961), pp. 21–40.CrossRefGoogle Scholar
Zilber, B., A note on the model theory of the complex field with roots of unity, available at www.maths.ox.ac.uk/∼zilber, 1990.Google Scholar
Zilber, B., Complex roots of unity on the real plane, available at www.maths.ox.ac.uk/∼zilber, 2003.Google Scholar